説明 semilogx (X,Y) は、x 軸の常用対数スケールと y 軸の線形スケールを使用して、x 座標と y 座標をプロットします。 線分によって接続された座標セットをプロットするには、 X および Y を同じ長さのベクトルとして指定します。 同じ座標軸セットに複数のグラフを書く意味 =06 05 log10 =log1006 05 =log1006log10 05 =loglog10 Y = b aX 両辺log 10 log 10 y =Y log 10 06 = b 05 = a log 10 x = X 対数をとると、傾き一定の直線になるはず xの指数が対数グラフ上の傾きになる →傾きを求めれば、指数が分かる とおく片対数方眼紙の使い方 片対数方眼紙はリニアの横軸と対数の縦軸からなる方眼紙です(もちろん横にして軸を入れ替えて使うこともできるわけですが). 自然現象の中には,指数関数 によって記述できる関係が多くあります この場合対数をとると と の
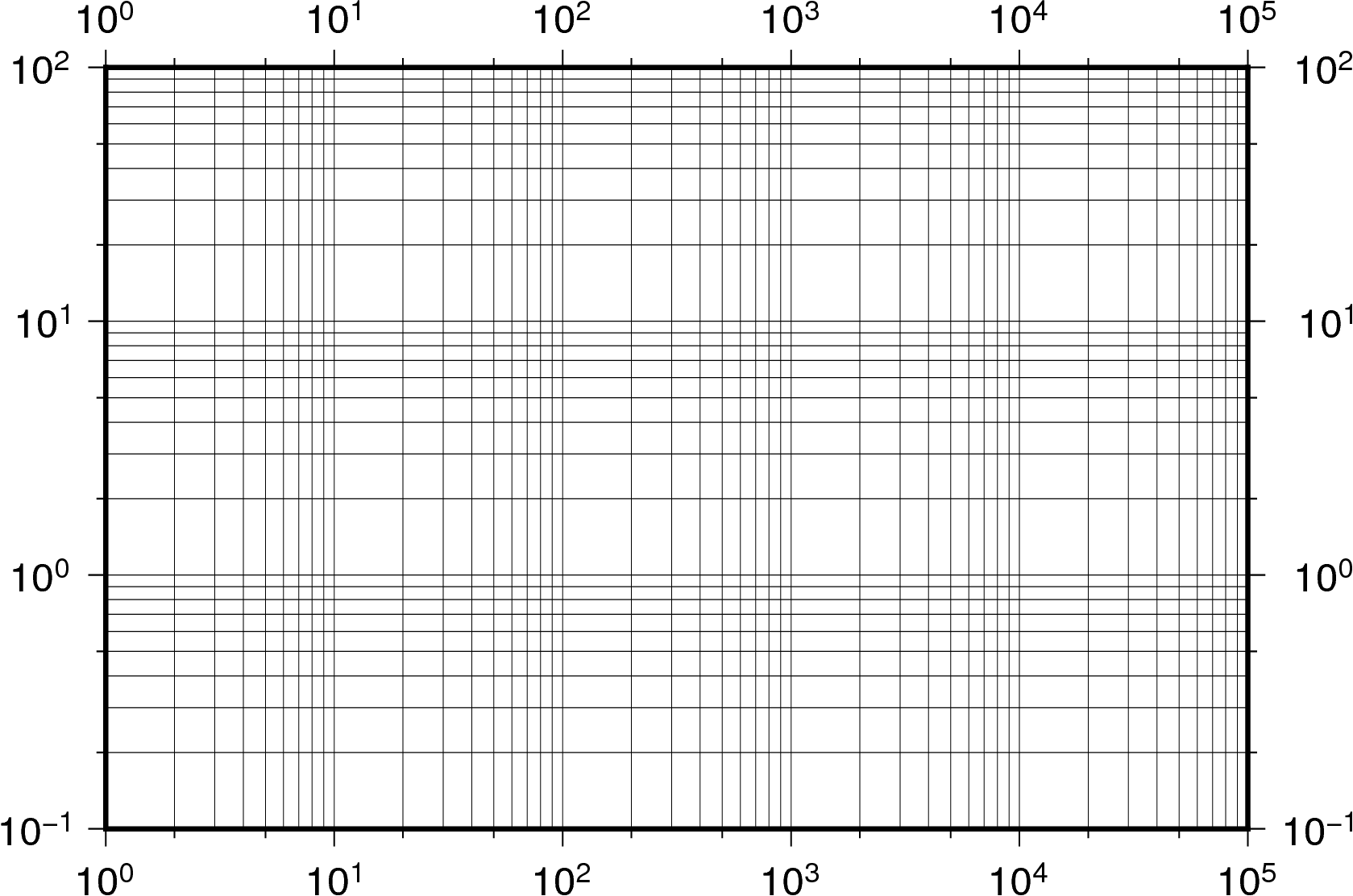
グラフ Logスケール 縦軸
片対数グラフ 傾き 意味
片対数グラフ 傾き 意味- · 片対数グラフ,両対数グラフの傾きの意味 対数グラフとは,対数目盛を使ったグラフのことです。 普通の目盛では「0から1」「1から2」が同じ1目盛分になりますが,対数目盛では,「1から10」「10から100」が同じ1目盛分になります。 このページでは,対数グラフについて解説しま片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説 片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾
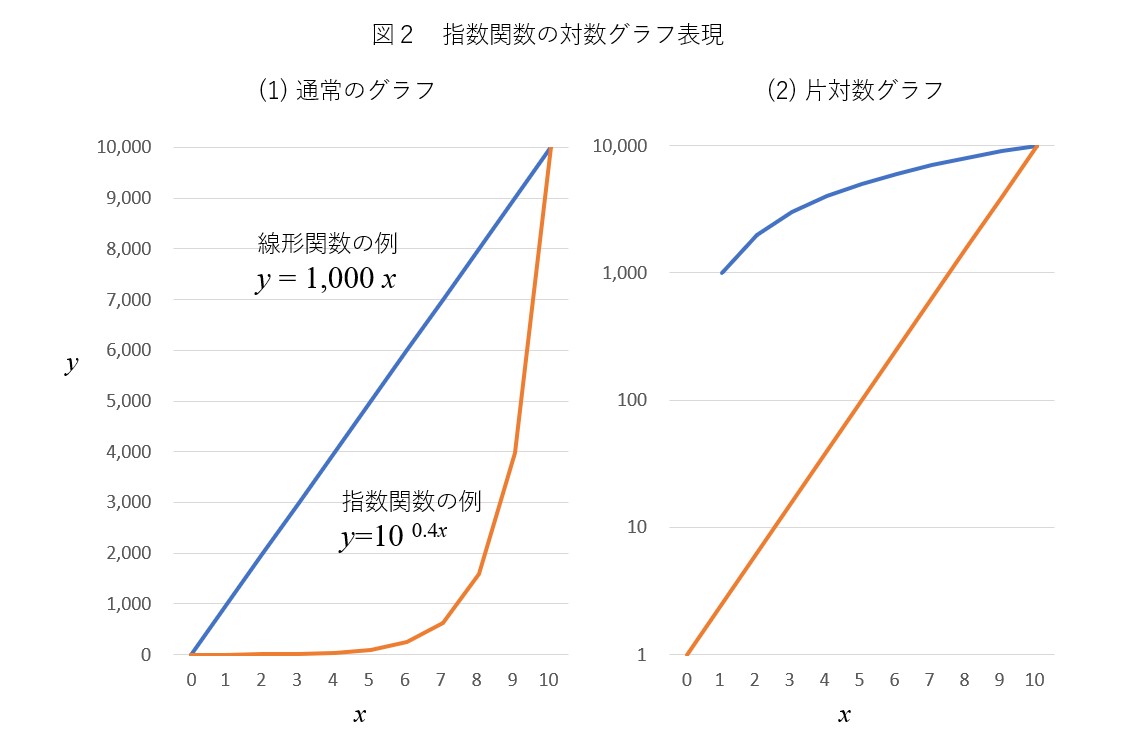



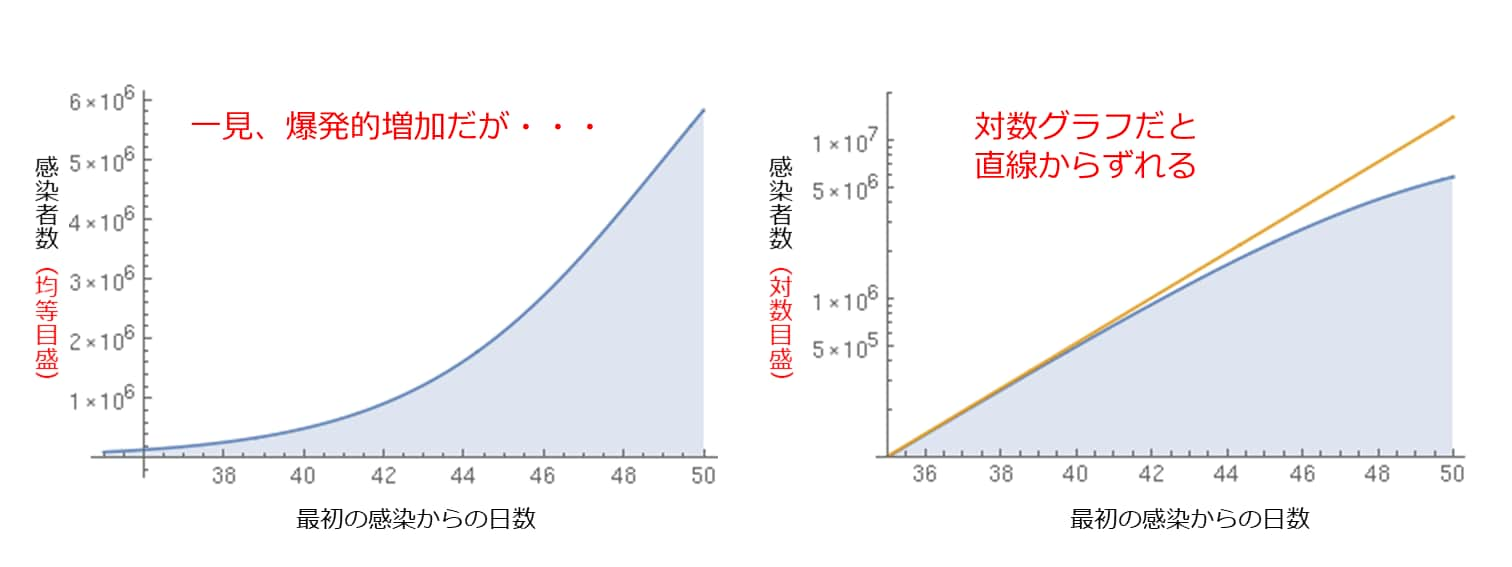
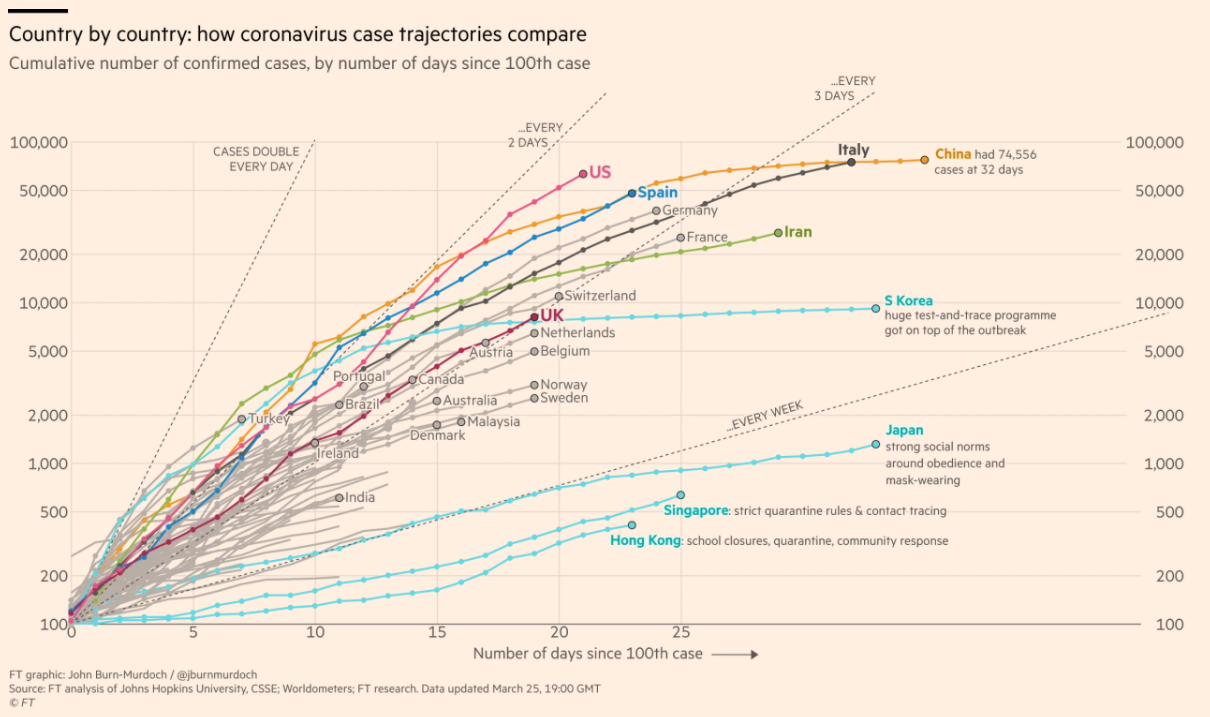
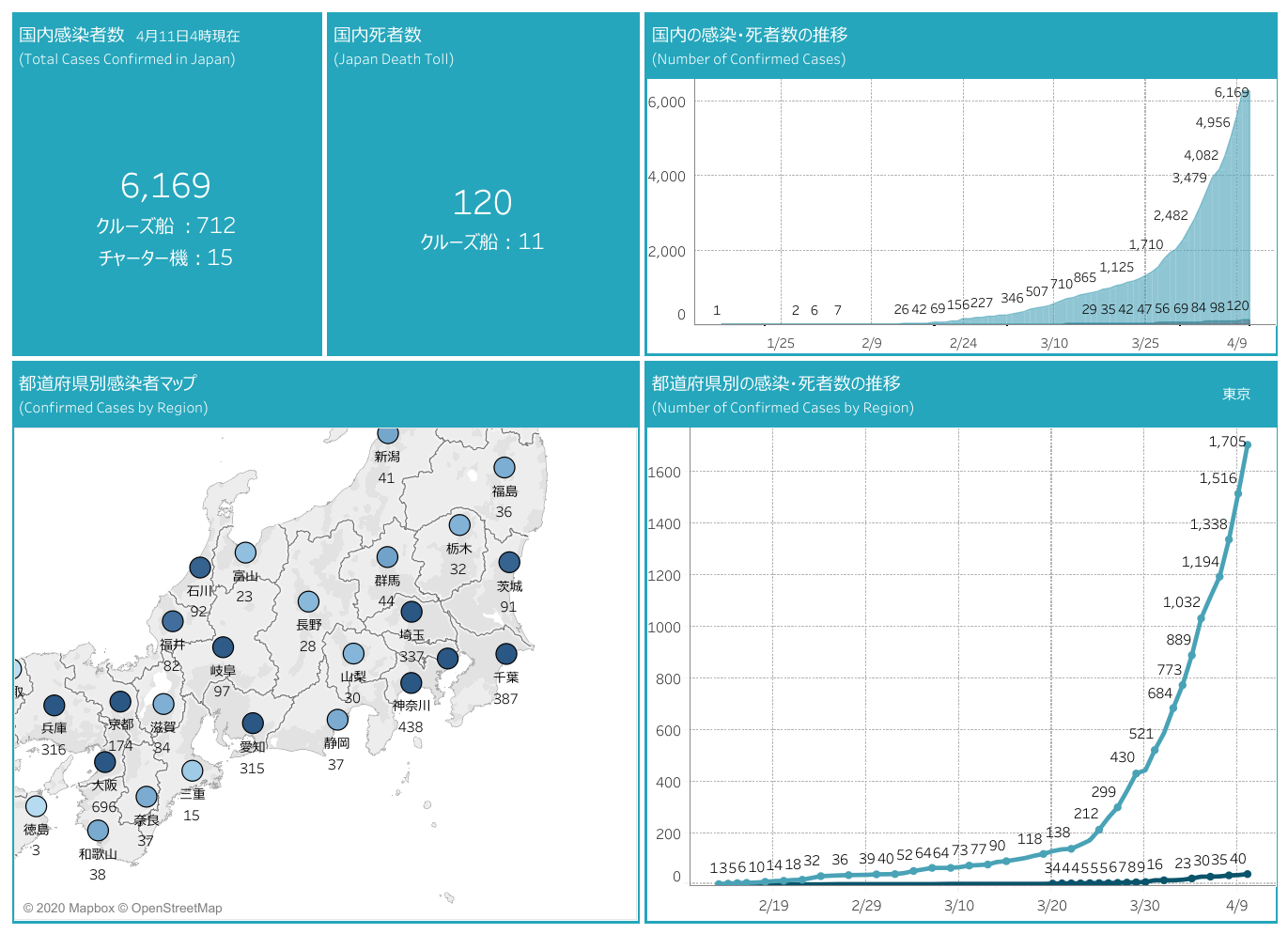
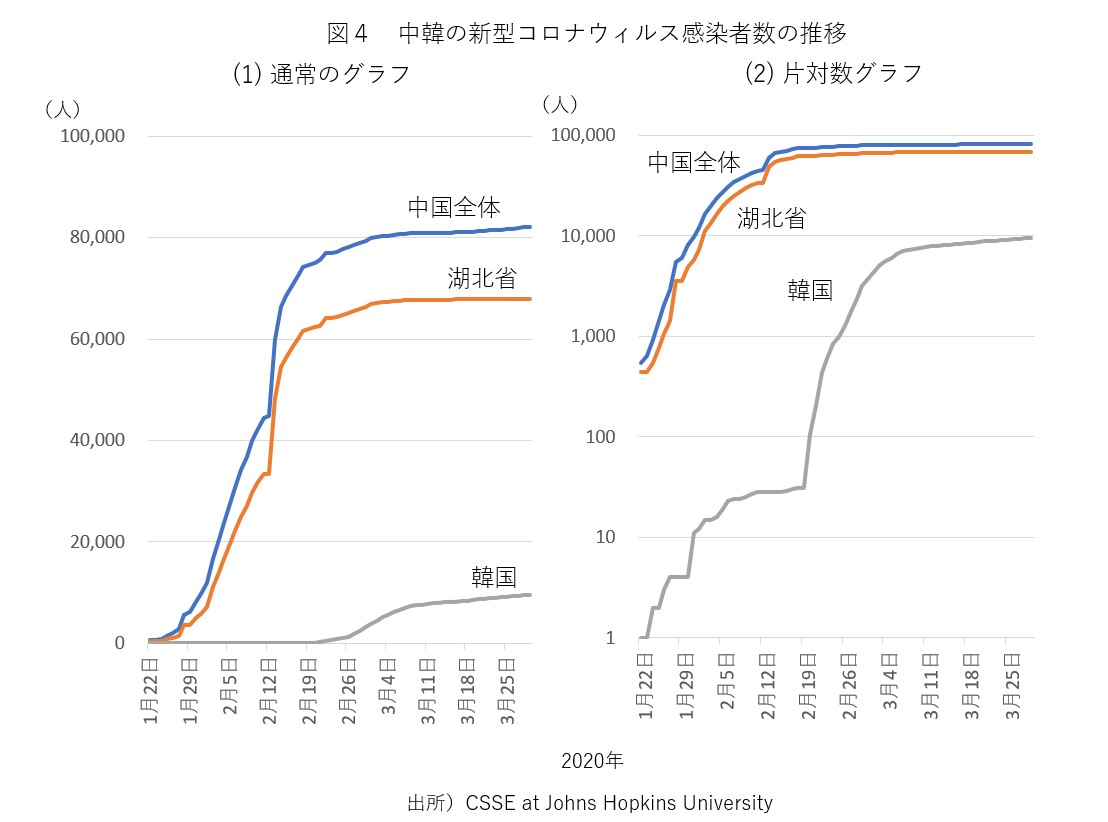
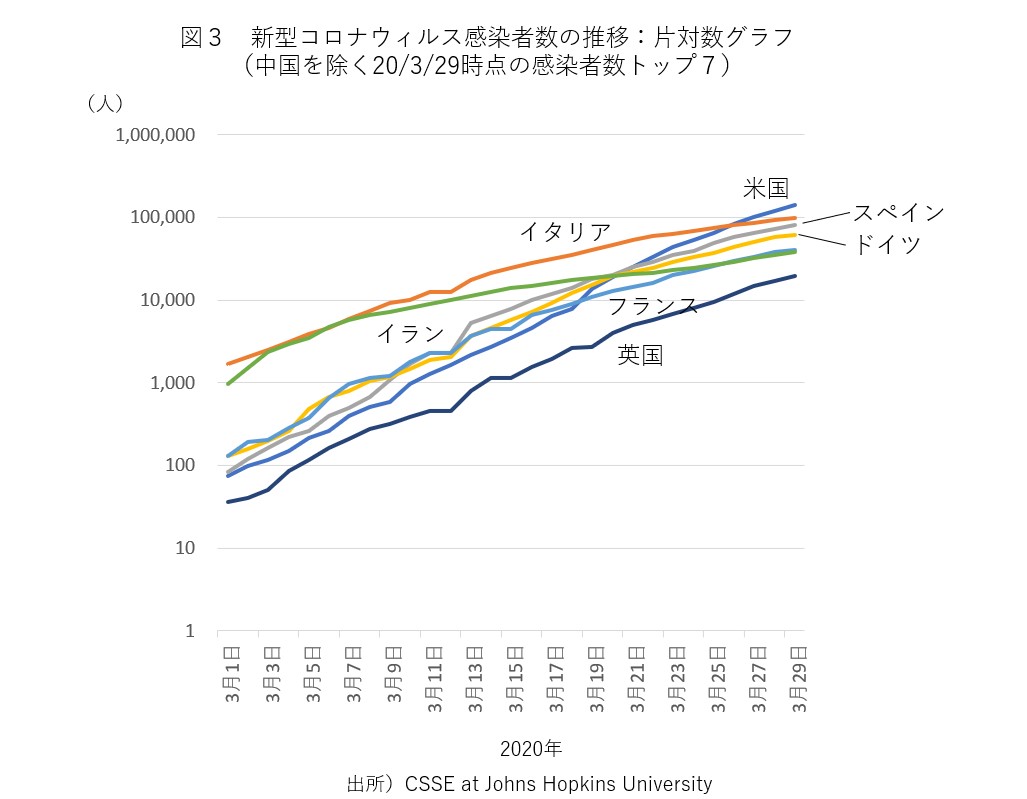
新型コロナウィルス 中国と韓国では初期には指数関数的増加が起きているものの あるポイントを超えると増加率が低下し始める 新型コロナ 増加が終息するポイント ビジネスジャーナル
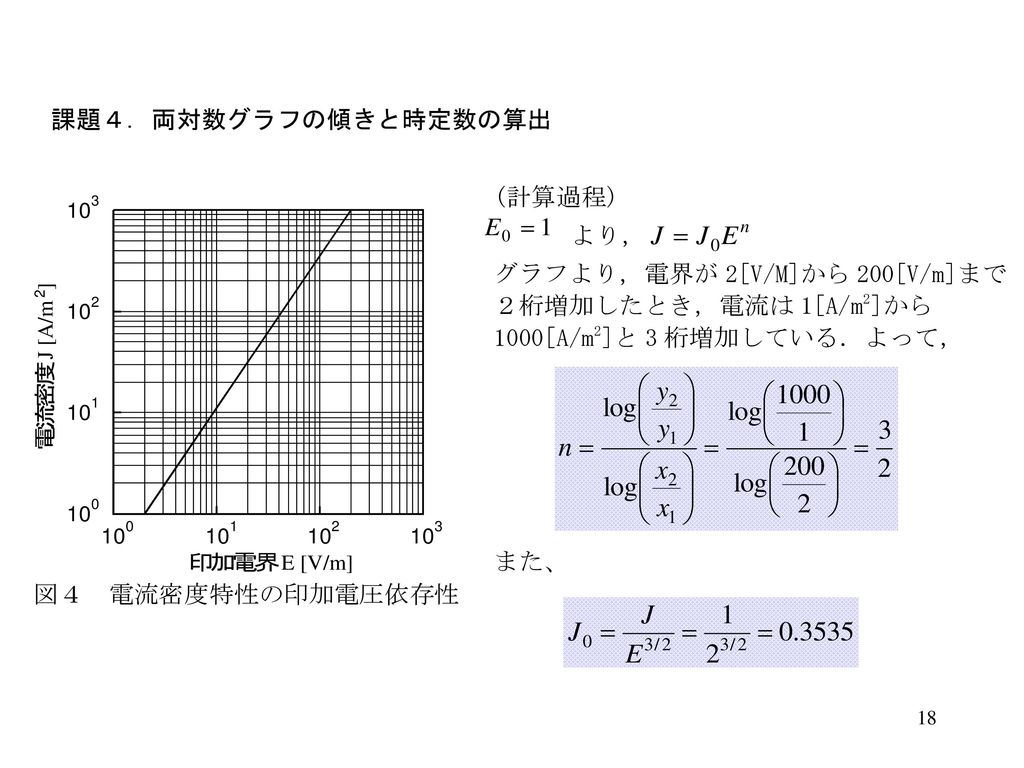
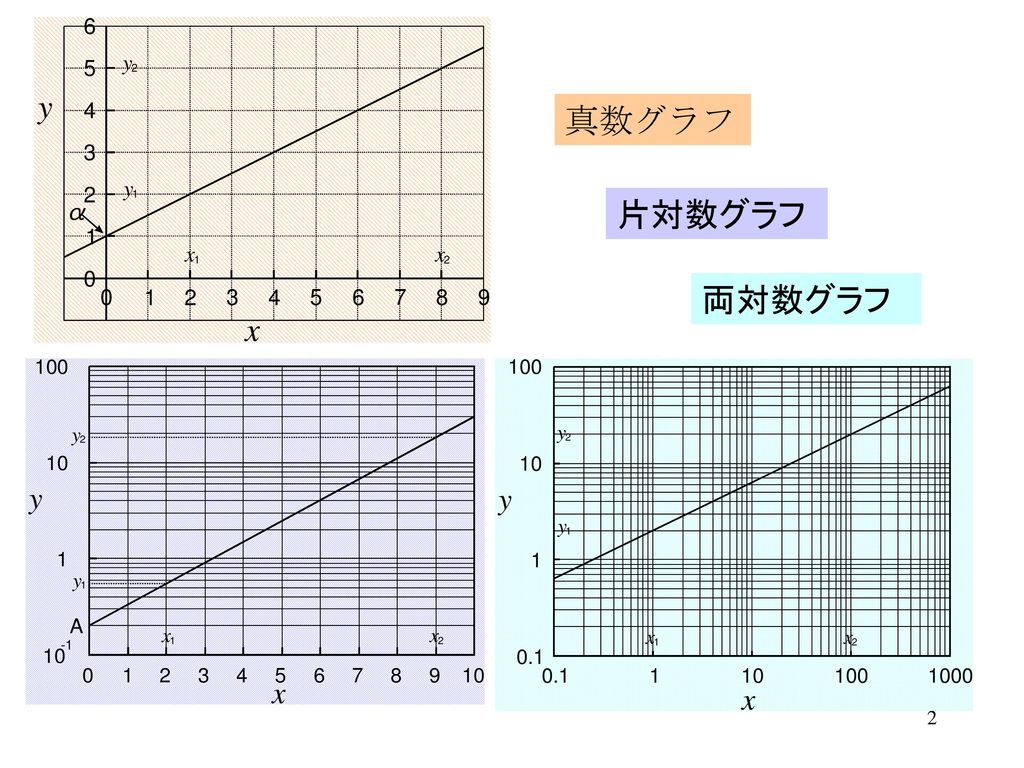
紙である。図3 の左は縦軸が対数目盛であ る片対数方眼紙,右図は縦軸,横軸がとも に対数目盛である両対数方眼紙である。 まり,片対数方眼紙に指数関数のグラフを 描くと,傾き 直線のグラフとなる 図 3 :対数方眼紙 (菅原正巳, 1951 ,p254)2.対数グラフで軸の桁の変わる線(上図の赤線)に目盛を書く. データの例として(1,0044),(5,0021),(10,0015),(15,0010),(30,0009)でやってみる. x軸の桁は10の0乗から10の1乗の2桁 y軸の桁は10の-2乗から10の-3乗の2桁両対数グラフは直線になります。しかも,直線の傾きは2です! つまり,2乗の「2」なわけです。 両対数グラフは文房具屋さんに注文すれば,買えます。きっと取り寄せでしょうけど。 他にも,片対数グラフというのもあります。 元に戻る
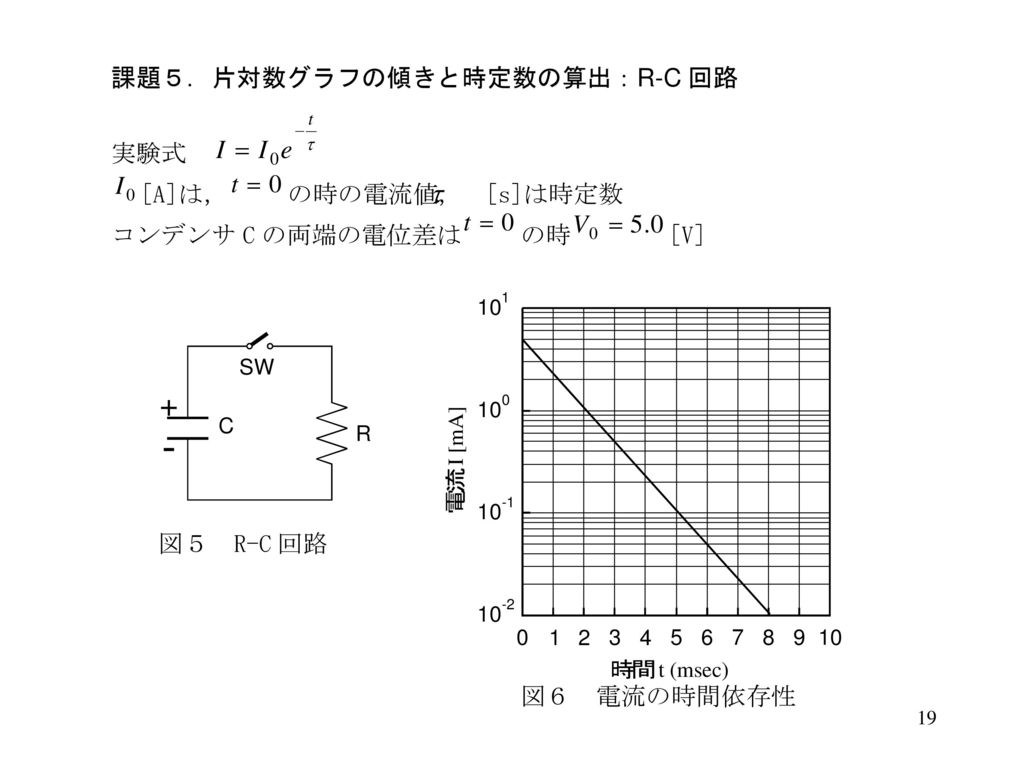
ただし \(I=b\1 e^{\1aV}\) のような関係式に対しては片対数グラフを用いることになるが、例えば底が \(10\) の対数をとると \(\log_{10}I=(a\log_{10}e)V\log_{10}b\) のように傾きに余分な因子 \(\log_{10}e\) が掛かることになるので注意しよう。したがって、\(1/T\) に対する\(\ln{k}\) の関係をグラフに描く(アレニウスプロット)と、傾きから活性化エネルギー\(E_a\) が求まる。このとき用いるのが縦軸のみ対数の片対数グラフである。 近似曲線 · 方対数グラフの場合(yが基本対数) y = ae^bxが直線を表す式となる 同じように両辺の対数をとるとLog(y) = Log(a) bxLog(e)となり ここに同様に代入して求めることができる (このeはネイピア数でなくてもよい) 傾きはbLog(e)である.
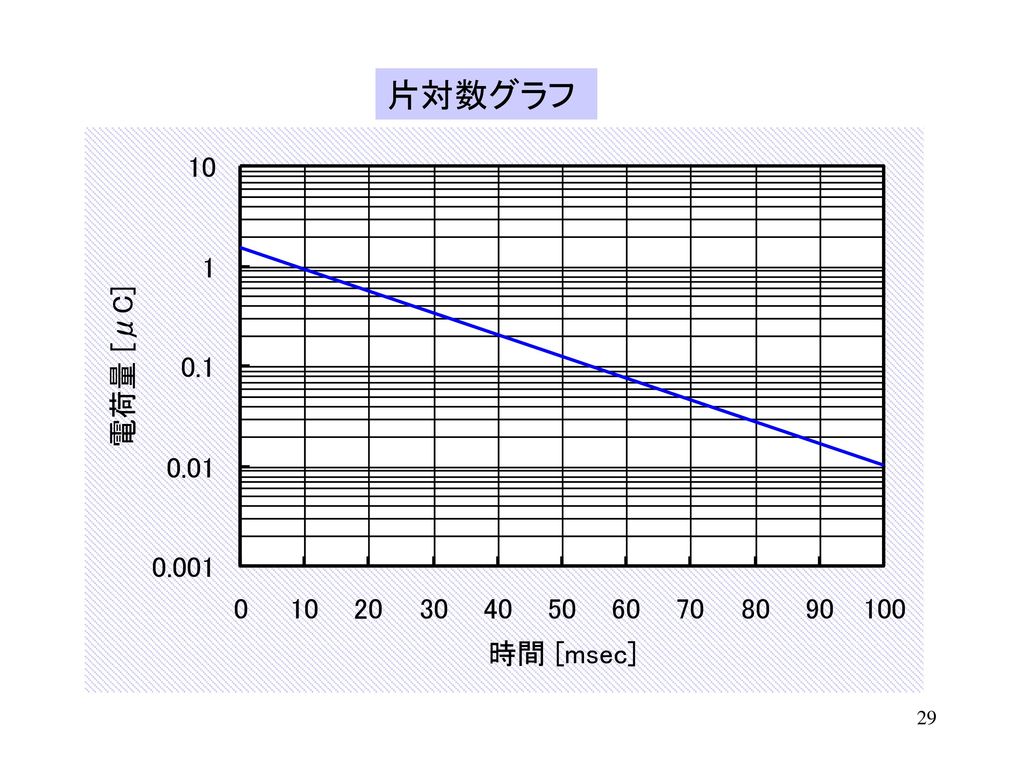
使います。片対数グラフとは片方の軸は1mm 目盛ですが、もう片方の軸が対数目盛になっているグラ フです。表紙には「片対数」とか「semilog」とか書いてあります。 では対数目盛とはなにか? 下の図を見てください。図の縦軸のように対数(log)をとった値の間隔 で目盛がふってあります。その他 片対数グラフと両対数グラフとは『読み方』や『傾き』の意味などを解説! 一般的によく見かける目盛は2点間の距離が 0,1,2,3,4,5・・・ のように数が 1ずつ増えたり 、 0,10,,30,40,50・・・ のように数に 10ずつ増えたり するような目盛となっています(この記事はこの目盛を 普通の(赤線)が直線になっていること、対数目盛であるy軸の数値の取り方に注意 片対数グラフ (かたたいすうぐらふ、semilog graph) とは、 グラフ の一方の軸が 対数スケール (縦を対数スケールとすることが多い)になっているグラフである。




理系大学生なら知っておきたいこと 片対数グラフの書き方 片対数グラフってどんなもの 山あり谷あり 学生生活




片対数グラフとは何か Training Day
1106 · log y = b x log a c log a {\displaystyle \log y=bx\log a\ c\log a} となる。 そこで横軸を通常の目盛りに、縦軸を対数目盛にすると、グラフが 直線 (傾き b log a {\displaystyle b\log a} , y切片 c log a {\displaystyle c\log a} の 一次関数 )になる。片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾 Excel エクセルで両対数グラフを作成する方法 両対数の傾きの意味は For more information and source, see on this link https①上の表のグラフを片対数グラフ用紙に折れ線グラフ で書く。 ②y=2 x と同じ傾きのグラフをその上に書く。 つまり、142万台(1945年)から順調に5年おきに2倍に (1950年142×2=284万台




薬物動態 消失半減期t1 2とグラフの読み方




12 号 半導体装置 Astamuse
· 手順2 傾きと切片を求める 片対数グラフでは,y座標の間隔が調整されているだけで値は変わってません.そのため,このまま直線の傾きを求めようとしても,傾き一定に 見えている だけなので増加率は場所によって異なってきます. ではどうするかというと,グラフから読み取れる2つの座標 ( x 1, y 1), ( x 2, y 2) のうち,y座標に常用対数 log 10 をとった上で · 片対数グラフ,両対数グラフの傾きの意味 高校数学の美しい物語 対数 グラフ とは, 対数 目盛を使った グラフ のことです。 普通 の目盛では「0 から 1」「1 から 2」が同じ1目盛分 · 片対数グラフ:縦軸を対数にするだけで直線になる 「縦軸を対数にするだけで直線になるような関係性がx x とy y にあった」 というのがポイントになるわけです。 そのような関係性にあるものは何かというと 指数関数 です。 例えば、下記のような関係式が成立しているような場合などが当てはまります。 y = ae−bx (1) (1) y = a e − b x これが上図の左の関係



Ew 基礎薬学完成 Egword




11 号 乗法九九学習具 Astamuse
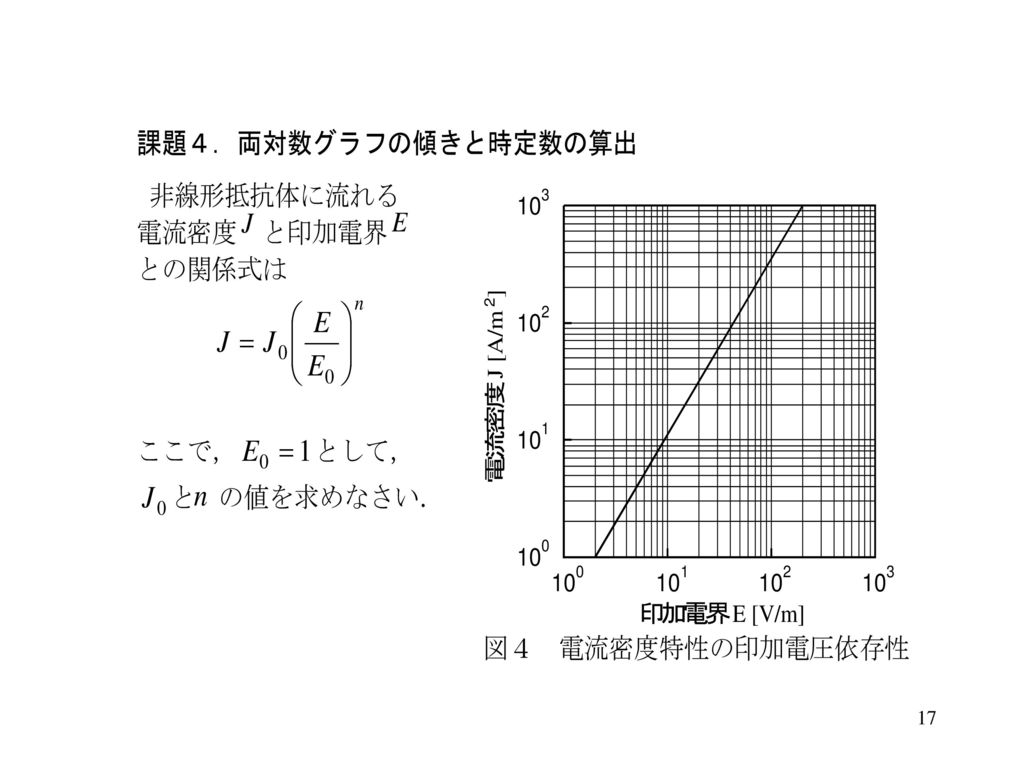
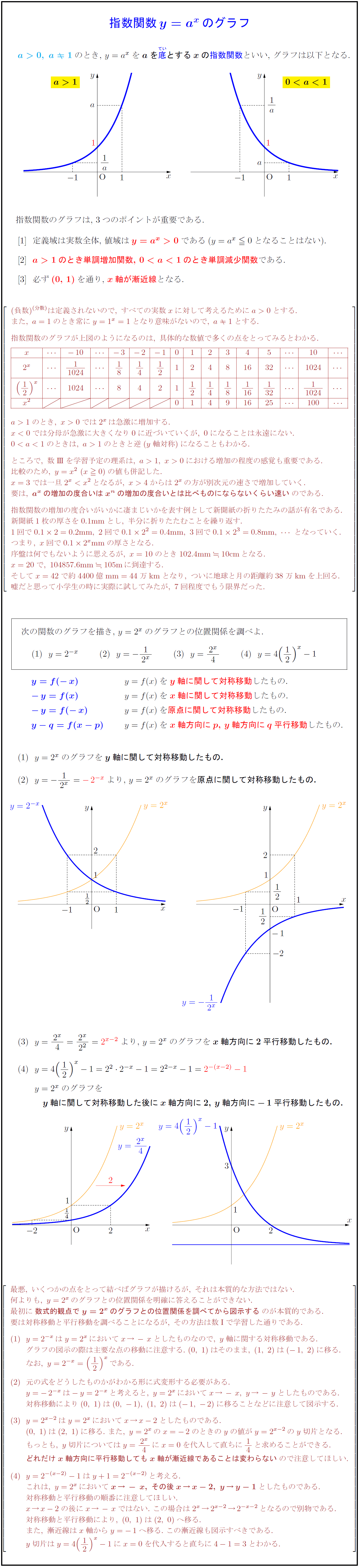
緑で描かれた 軸と 軸で傾きを読みとると、横軸の が1増えると縦軸の は2増えているので傾きは2、横軸 で縦軸 は 01程度であるので切片は約01である。表1の両対数グラフの行から 、 であり とほぼ元の関数の を読みとることが出来る。下の図では、対数 log 10 = 1を長さ100mmに対応させて表している。 例 log5はA点の位置に点を取れば、log5=になる。B点は log40 である。片対数は縦軸、横軸の目盛り方がどちらか一方が対数目盛であり、両軸とも対数軸の場合は両対数と言っている。両対数グラフでの散布図作成と線形近似の方法 on Excel 準備 X軸に入れるデータセット(logR)、Y軸に入れるデータセット(logN)は、それぞれ生 のR, Nの値から常用対数に書き直しておく。 ※使う関数は「LOG10」 散布図 1 データの入力されていないセルを選択。



各国のcovid 19状況の分析 03 22時点 その1 ホットスポットはポルトガルとアメリカ 計測マニア イワサキ




アレニウス プロット 傾き 活性化エネルギー e と頻度因子 A について先週反応速度の実験を行いまし
· 片対数にとったということは、y軸がlogだと思います。 傾きは、y軸の変化÷x軸の変化なので、 y x 3 1 5 2 7 3 のとき、(53)÷(21)をします。 すると 2 と言う値がでると思います。これが傾きです。 · 片対数グラフというのは、縦の軸か横の軸の片方の目盛りが等間隔の目盛りではなく「対数の目盛り」になったグラフです。 片方の軸なので、縦と横のどちらを対数にしてもOKですが、縦を対数軸にすることが多い気がします *1 。 · 片対数グラフ は 本記事では、これらの素朴な疑問に答えつつ、最終的に片対数グラフの意味 を満たす値であった。これはグラフ的に解釈すると、\( x=0 \) における接線の傾きが \




片対数グラフはやめてほしい Qiita
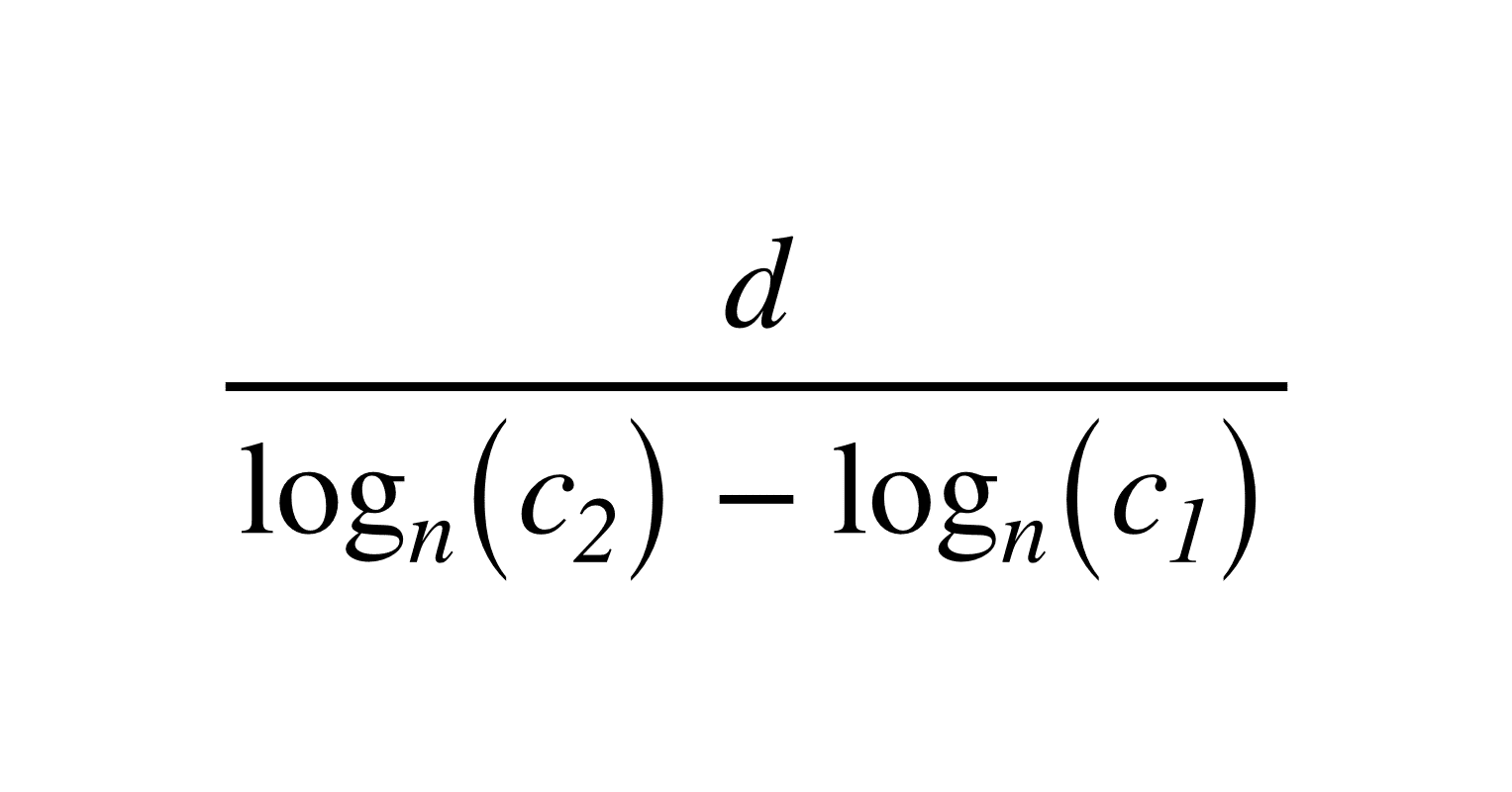



倍になるのはいつか 緒方 壽人 Takram Note
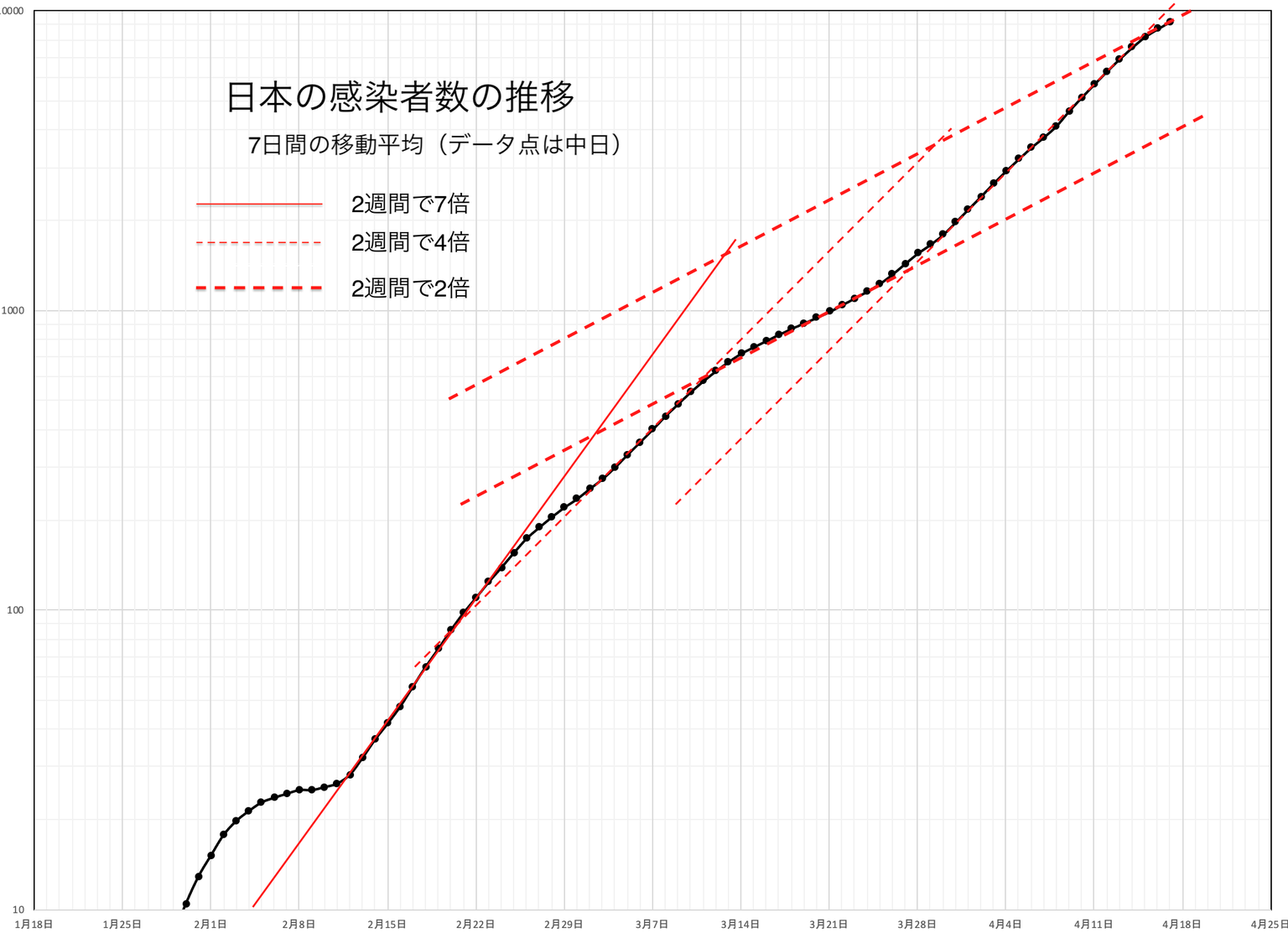
2504 · 通常のグラフでは見えてこなかった2週目、4週目のような 絶対数がまだ少ないときでも差もはっきり見えることができます。 また 対数グラフで指数関数的に増加するものを、直線で表すことができる ので、 この増加率の違いをいち早く気づくことができ、 将来の推移の見立てが可能 となります。 増加率の変化もこのグラフの傾きで見ることができます。下図のようなデータを使って片対数グラフと両対数グラフを作成してみます。 データリストの例 b列は1~100の整数値、c列は y=x^2 、d列は y=1/x^2 の計算値です。 散布図を作成する 散布図の作成手順片対数グラフとは、「x軸: 普通の目盛 、y軸: 対数目盛 」や「x軸: 対数目盛 、y軸: 普通の目盛 」のようにx軸またはy軸の 片方 が対数目盛となっているグラフのことを指します。 片対数グラフは英語では「SemiLog Plot」または「SemiLog Graph」と書きます。 両対数グラフ 両対数グラフとは、「x軸: 対数目盛 、y軸: 対数目盛 」のようにx軸とy軸の 両方 が対数



曽呂利新左衛門 雲外蒼天
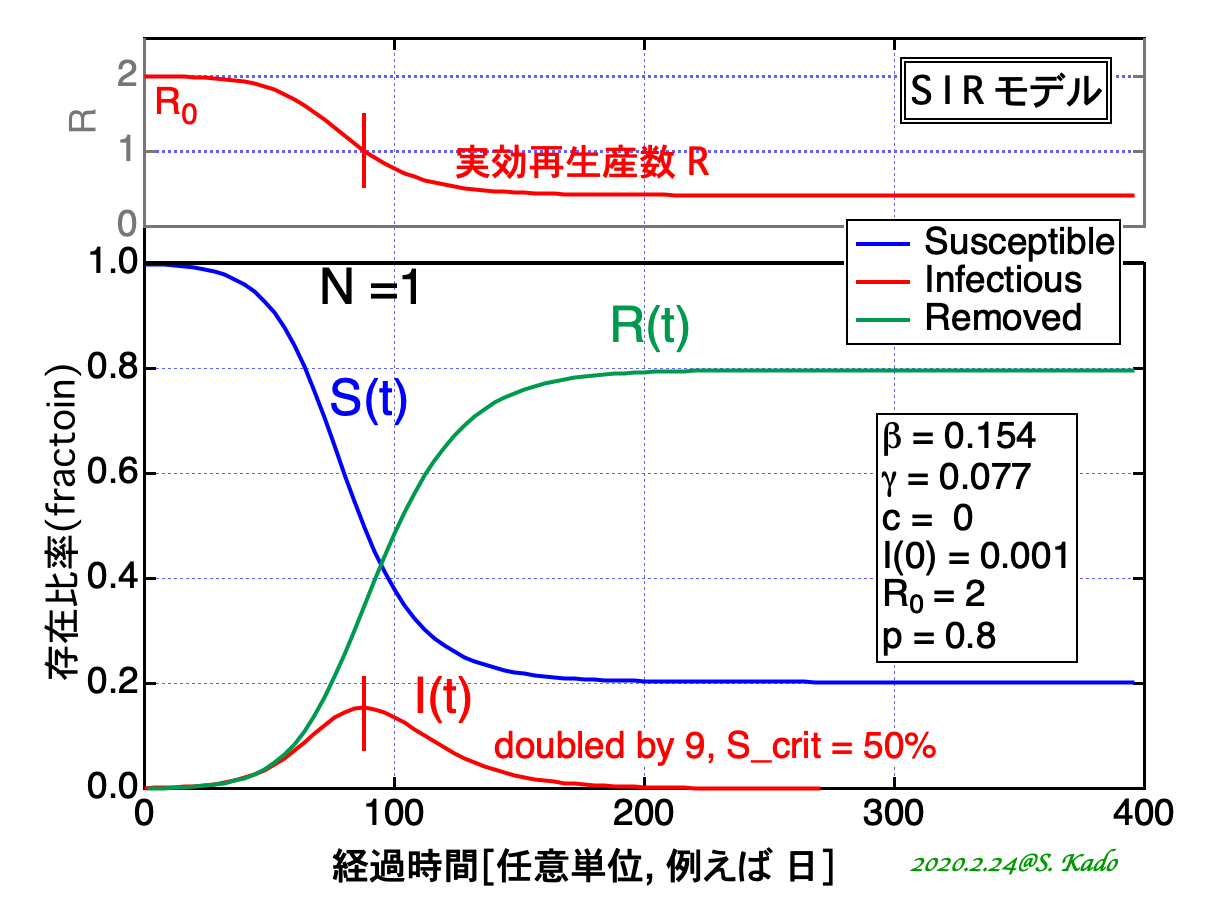



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21
· 片対数グラフと傾き・切片の出し方 大学の物理実験の前に、準備としてグラフの書き方を教わっています。 そこでの練習問題なんですが、V=V0e^αtという式があり、いくつかの数値と計測回数が書いてありま · 片対数グラフ・両対数グラフとは?読み方・書き方・使い方を解説! 2101 テイラー展開とは?イメージ・式の意味 · これが片対数のグラフです。 グラフとしてはy=ax+bと同じです。 勾配はa,切片はbです。 切片はVoではありません。b=lnVoです。 グラフからbが分かればVoが分かります。Vo=e^b です。 Y=AX^α であれば lnY=lnA+αlnX



各国のcovid 19状況の分析 03 22時点 その1 ホットスポットはポルトガルとアメリカ 計測マニア イワサキ




エクセル 一次 関数 グラフ
対数グラフダウンロード こちらからpdfファイルがダウンロードできます。 種類をクリックすると、ダウンロード画面が表示されます。用紙サイズはa4です。 片対数グラフLog グラフ変換, 片対数グラフ,両対数グラフの傾きの意味 ※対数の底は何でも構いませんが(底の変換公式よりスケールが変化するだけ)今回は常用対数で説明します。この記事では $\log_{10} x$ を $\log x$ と書きます。 なお1106 · カテゴリマスター /6/11 1845 y=aexp(bx) (1)のグラフが直線になることです。 直線の傾きがbです。 自然界や工学の世界では(1)の式で表される現象が多く、そのもっとも重要なファクターがbで、これが簡単に求められることで片対数グラフは非常に有効なデータ解析ツールです。 1人がナイス! しています ナイス!




グラフ Logスケール 縦軸




Jpa Dosage Form Containing Oxycodone And Naloxone Google Patents
片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語 For more information and source, see on this link https//mathtrainjp/loggraph 対数グラフとは 読み方 書き方 使い方を具体例で解説片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語 For more information and source, see on this link 片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾小野測器減衰をあらわす係数の意味と求め方 (page1) 1 はじめに 機械が稼働していれば振動は避けられない現象ですが、振動は不快なだけでなく故障の原因ともなり、甚だしい場合には機械の破壊に至ることもあります。 振動が起きてから対策を施してい



7 1 そもそもa Ab B級動作とはアイドリング電流や動作時の電流変化により分けられます C級動作なんて動作条件もありますが C級動作は高周波の世界の話でありオーディオアンプでは使いません 近年では何故かd級アンプなんて物もあります




新型コロナウィルス 中国と韓国では初期には指数関数的増加が起きているものの あるポイントを超えると増加率が低下し始める 新型コロナ 増加が終息するポイント ビジネスジャーナル
· 片対数グラフの場合は、片方だけ対数にしたグラフですが、 y=e^nxで考えてみると、両辺の自然対数をとって、 log (y)=log (e^nx)=nx・log (e)=nx Y=log (y), X=x の片対数グラフに描くと、 Y=nX よって、傾きnはyが底eのnx乗に比例していることを示す。グラフから読みとれる傾きが 、切片が である。このことから読みとった傾きと切片から元の関数の と を求めることが出来る。 対数関数の式を変形する。 を代入し、両辺の10の対数を取る。



エクセル 片 対数 グラフ 作り方




文系のための対数グラフの読み解き方 算数だけでわかる Youtube
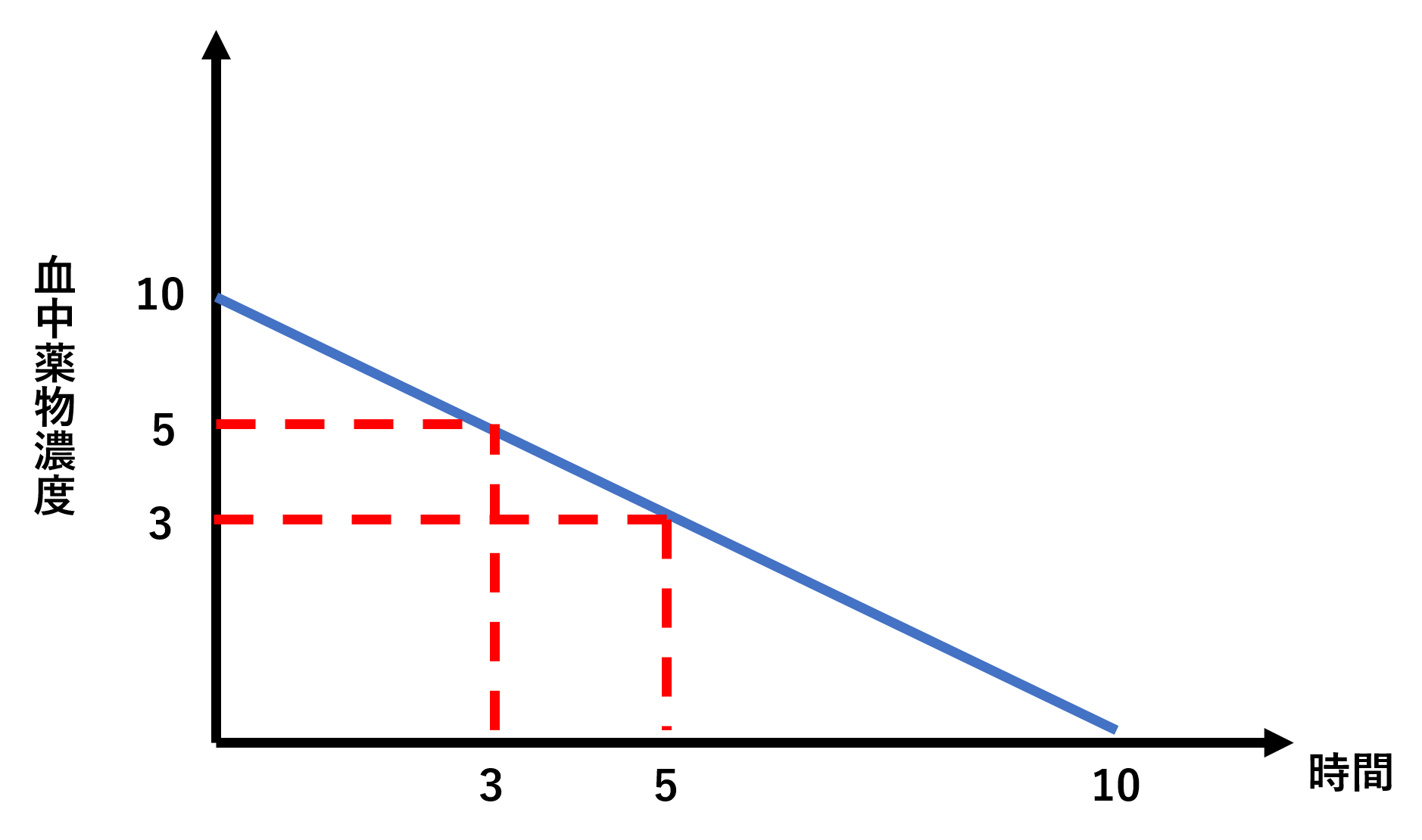



薬物動態 消失半減期t1 2とグラフの読み方




高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ




片対数グラフとは何か Training Day



片対数グラフとは何か Training Day




グラフ Logスケール 縦軸
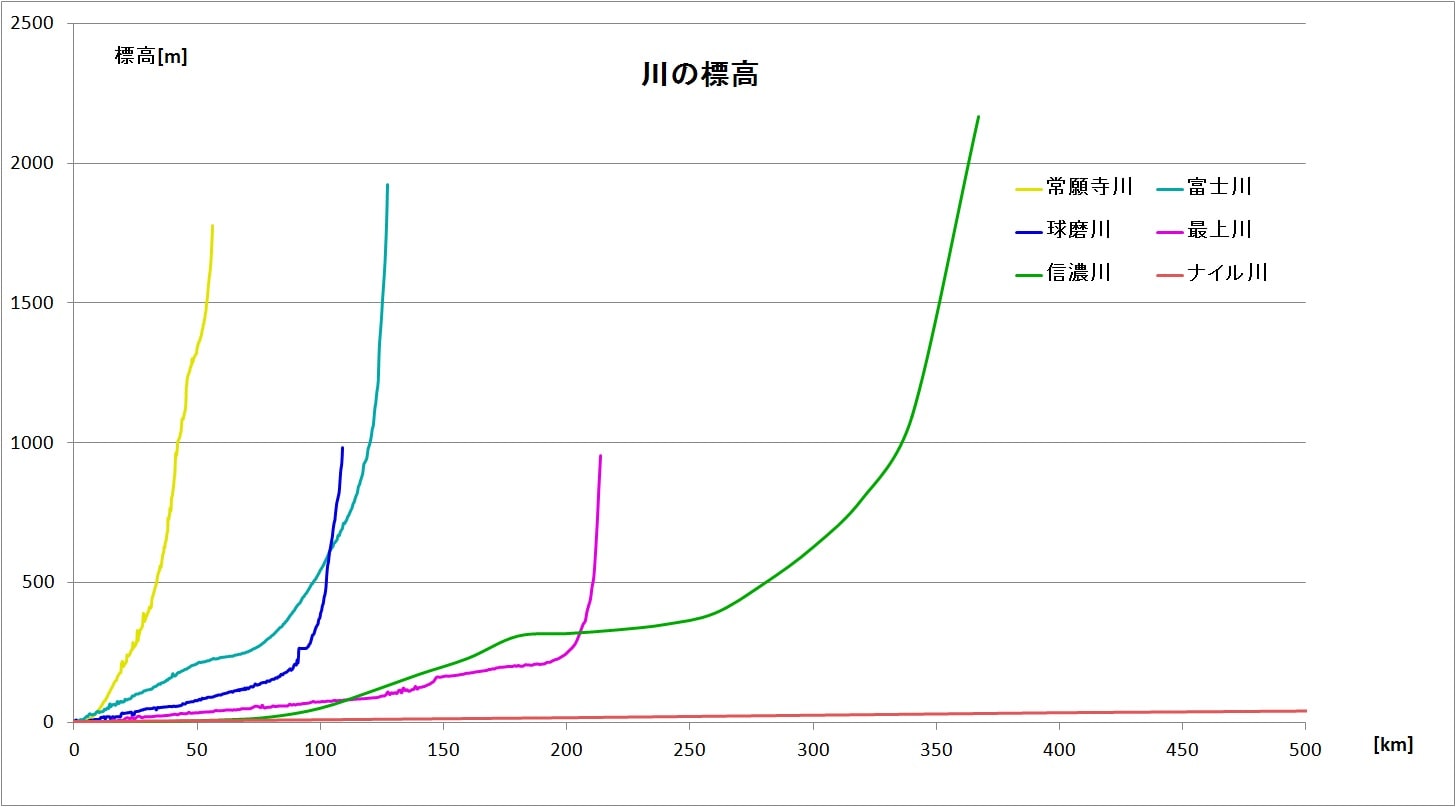



勾配 意味 グラフ



ログスケール エクセル




片対数の意味 用法を知る Astamuse
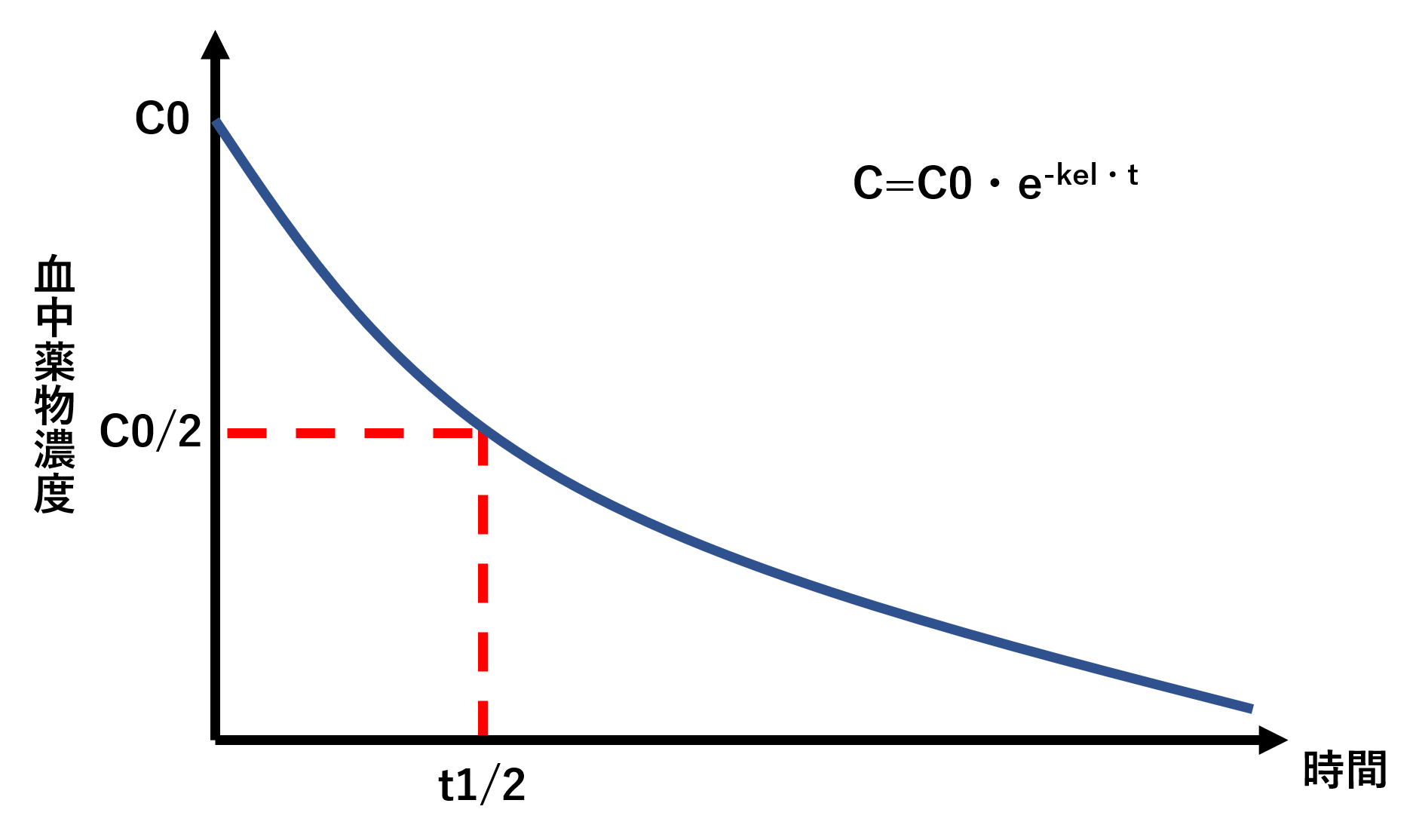



薬物動態 消失半減期t1 2とグラフの読み方



エクセル 片 対数 グラフ 作り方




Web版 Fxtradeのチャートのスケールの設定 Oanda Fx Cfd Lab Education オアンダ ラボ



電気基礎実験 グラフ処理 Ppt Download



折れ線グラフの作成 Blog メディア情報研究室 村上真研究室 東洋大学総合情報学部




片対数




Mizuno Yoshiyuki 水野義之 先日 統計学入門 の授業の中で 対数 をどうしても説明する必要があった それで スライド1枚で 対数とは を書いてみた 京都女子大学の学生さんにも 割と好評だったので 公開します ご笑覧下さい



片 対数 グラフ 書き方 整流用ダイオードの順方向特性について測定を行い 片対数グラフを用



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先




ボード線図 ゲイン線図とは 書き方から学んで理解する 理系大学院生の知識の森



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ




第97回薬剤師国家試験172問 解説




理系大学生なら知っておきたいこと 片対数グラフの書き方 片対数グラフの使い方 山あり谷あり 学生生活



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先
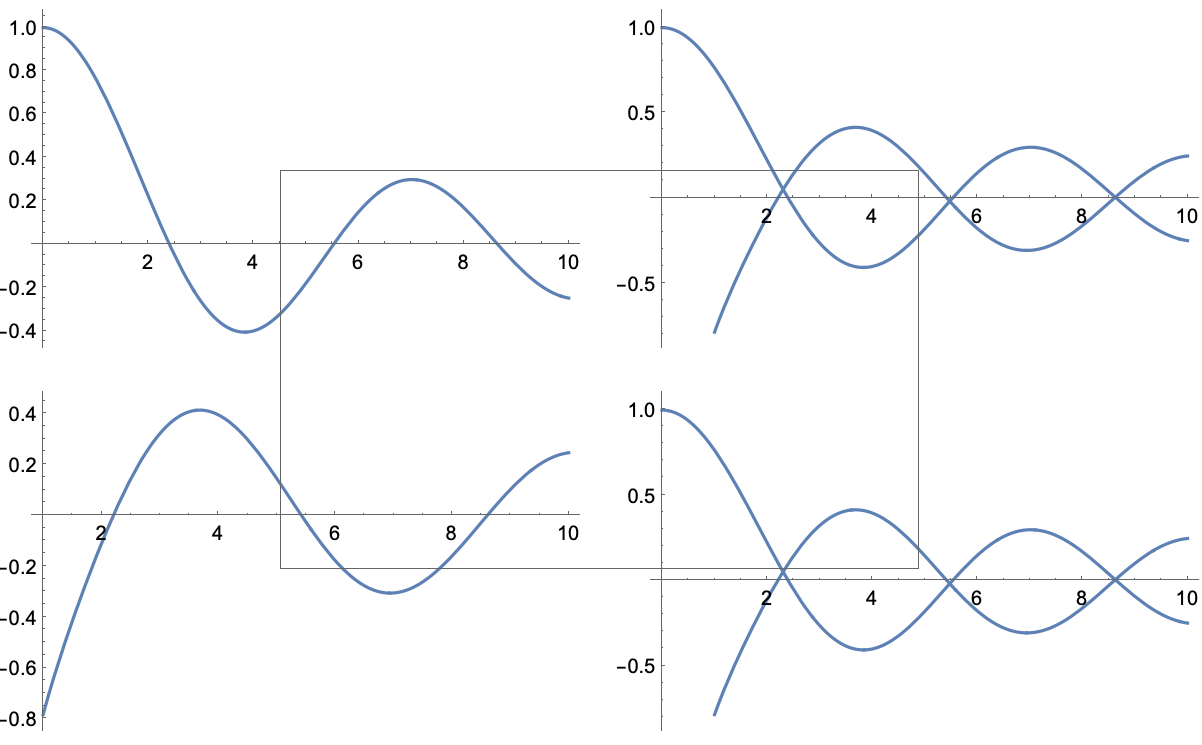



グラフィックスとサウンド Wolfram言語ドキュメント




11 号 乗法九九学習具 Astamuse




Tkyon Octave グラフの例 編集例




バトラー ボルマー式 Wikipedia
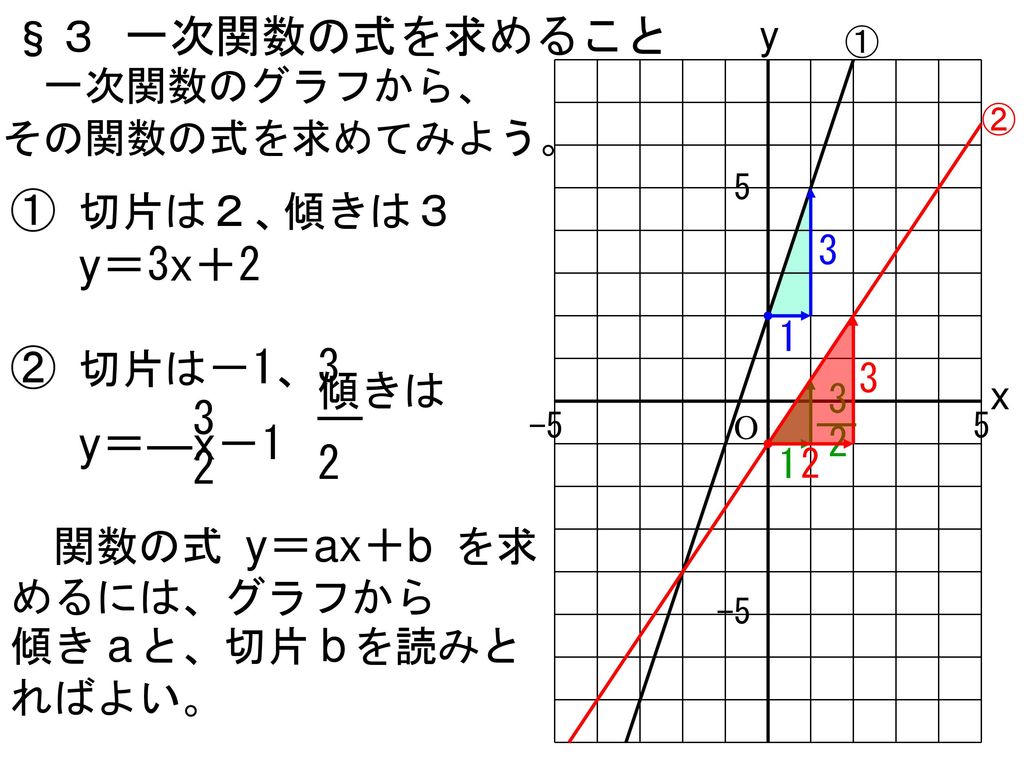



エクセル 一次 関数 グラフ




傾き 微分 を求めたい 添付写真の三角波の傾き Dvi Dt をグラフか Okwave
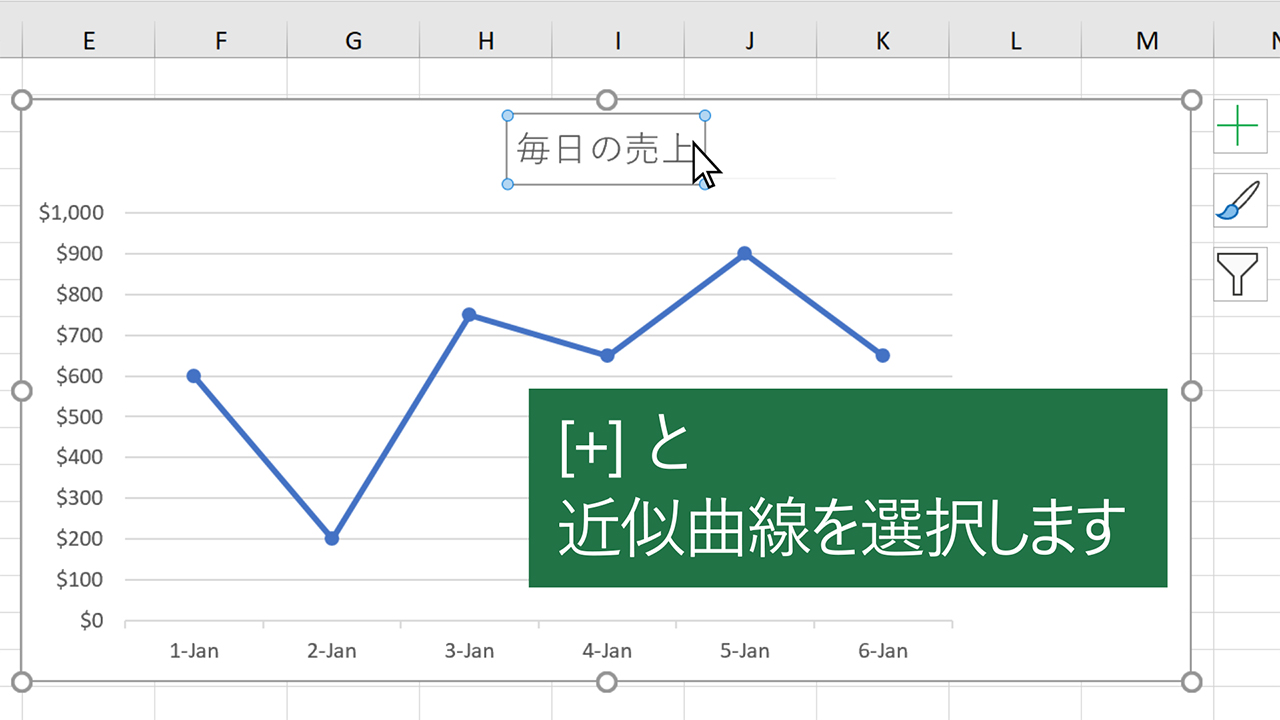



グラフに近似曲線や移動平均線を追加する Office サポート



新型コロナウイルスの感染者数を対数グラフを描くとわかること オーディオデザインのコラム
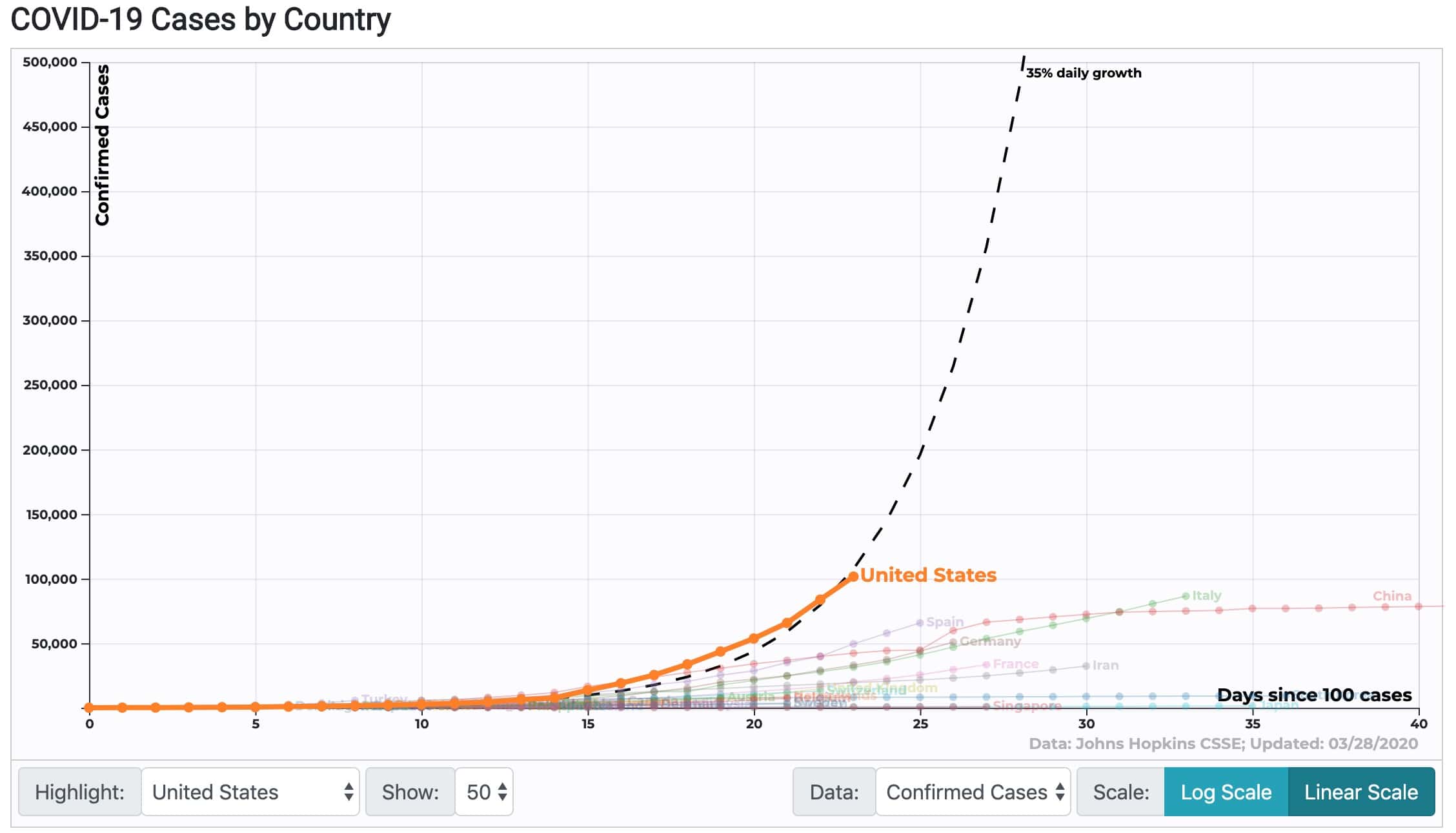



新型コロナウィルスで考える指数関数的な変化と自然現象 科学のネタ帳
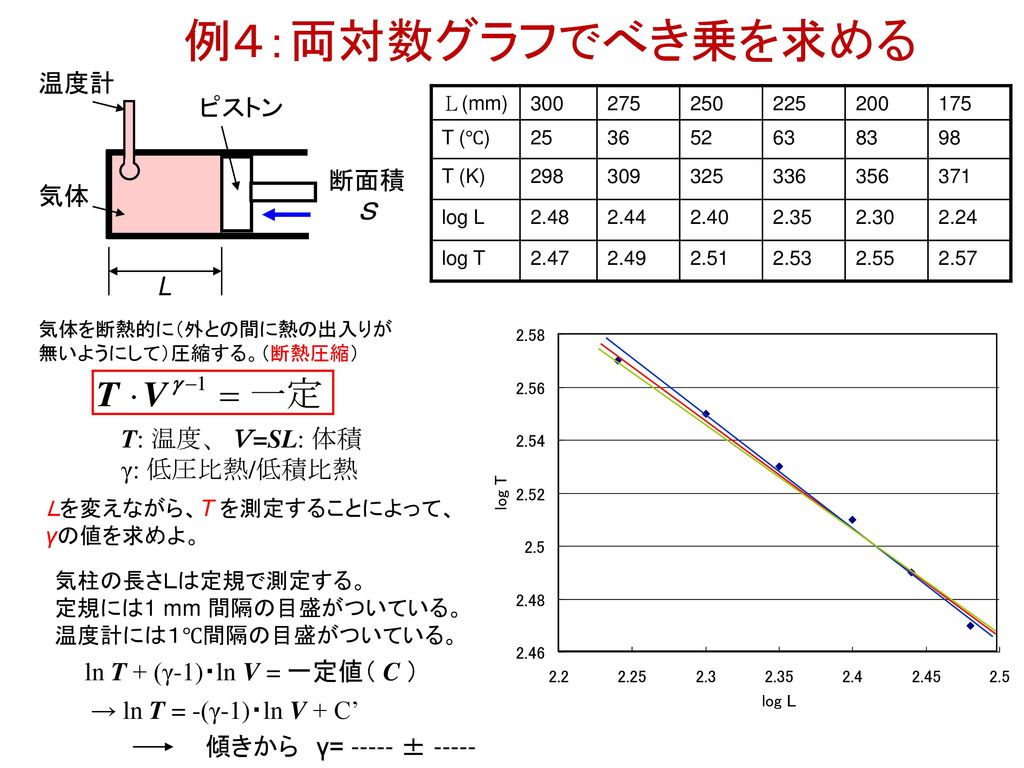



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download




対数 グラフ コロナ ビデオ ニュース



スライド 1



片 対数 方眼 紙



新型コロナウィルス 中国と韓国では初期には指数関数的増加が起きているものの あるポイントを超えると増加率が低下し始める 新型コロナ 増加が終息するポイント ビジネスジャーナル



曽呂利新左衛門 雲外蒼天




Tkyon Octave グラフの例 編集例




エクセル 片 対数 グラフ 作り方




人工曲線 の立て直し 余生庵 カラスの晴耕雨 読ぶろく クンセイが肴
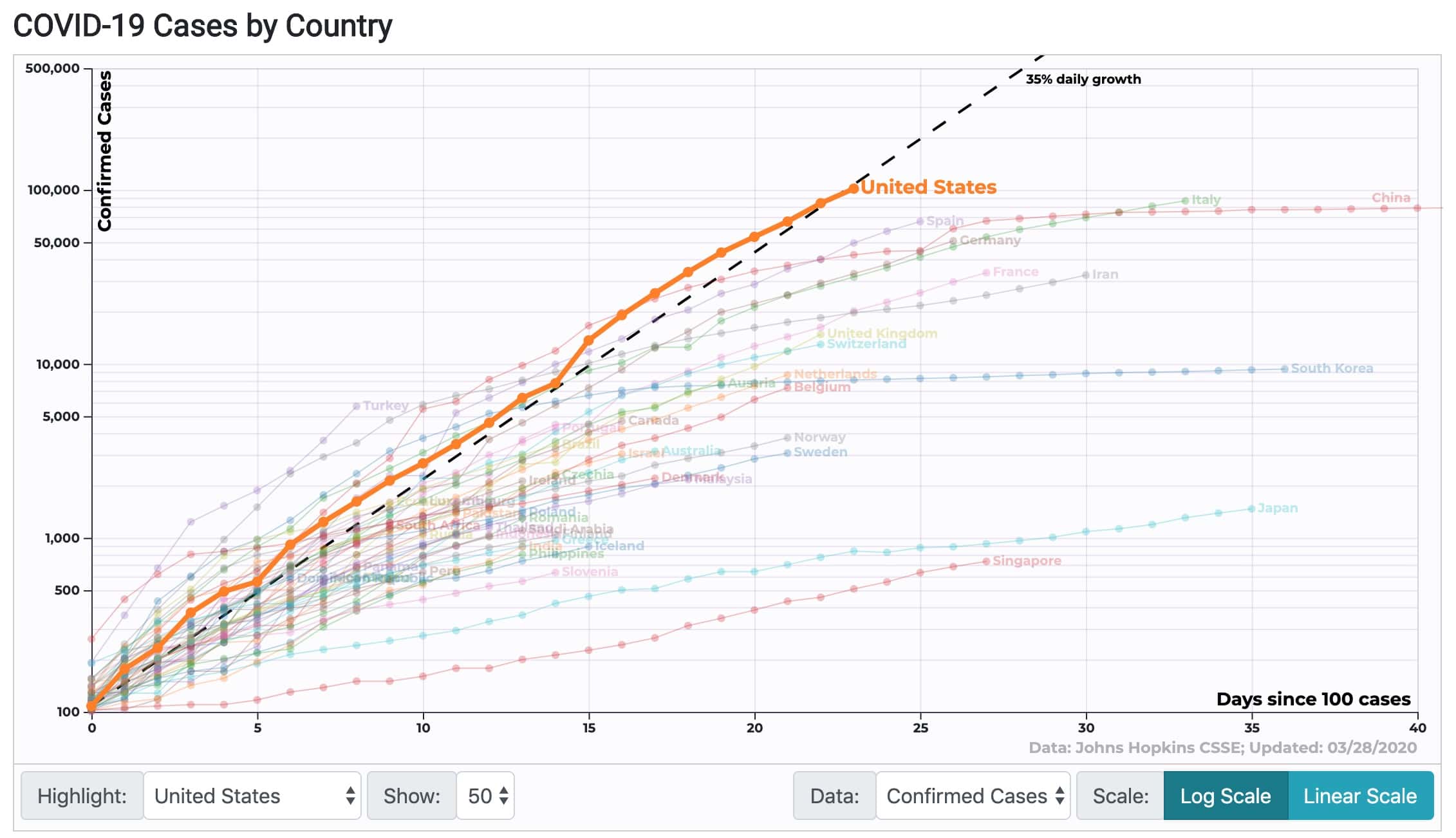



新型コロナウィルスで考える指数関数的な変化と自然現象 科学のネタ帳




片対数グラフ
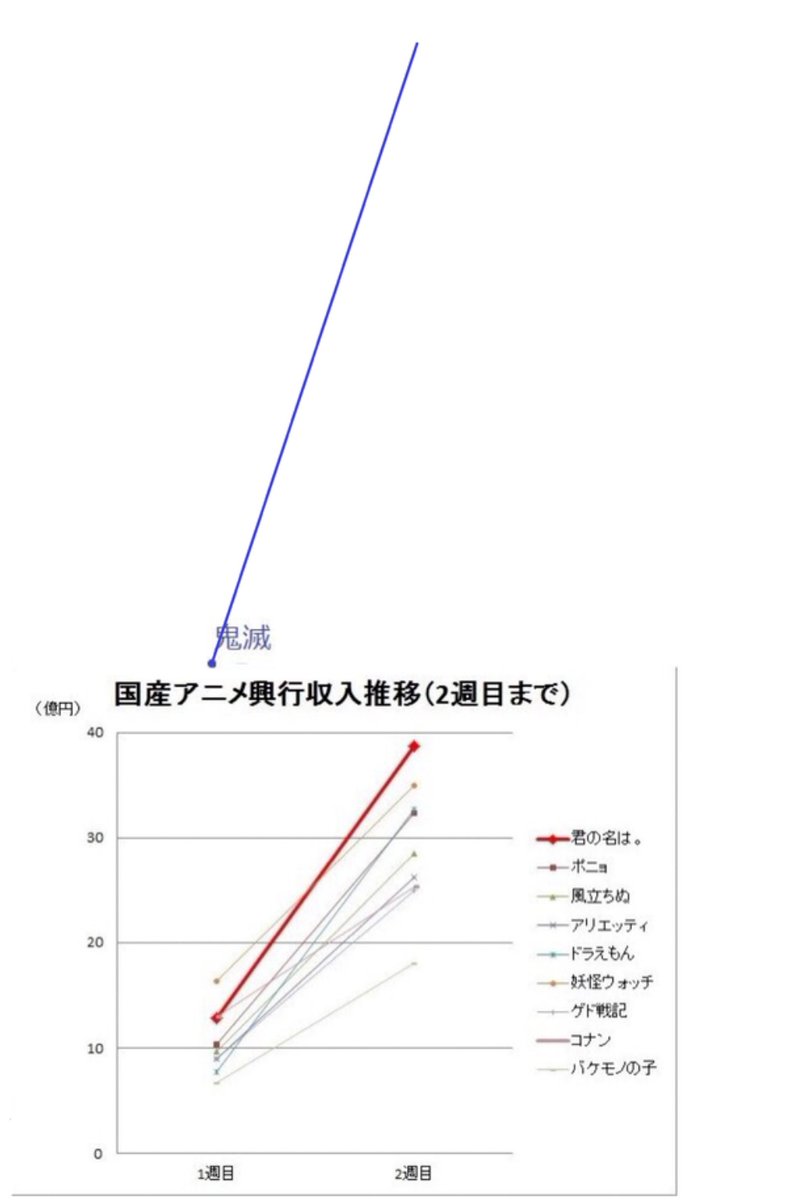



劇場版 鬼滅の刃 興行収入グラフが更新されたが なんだかおかしいことになっていた 座標バグってますよ 冗談みたいなグラフ Togetter
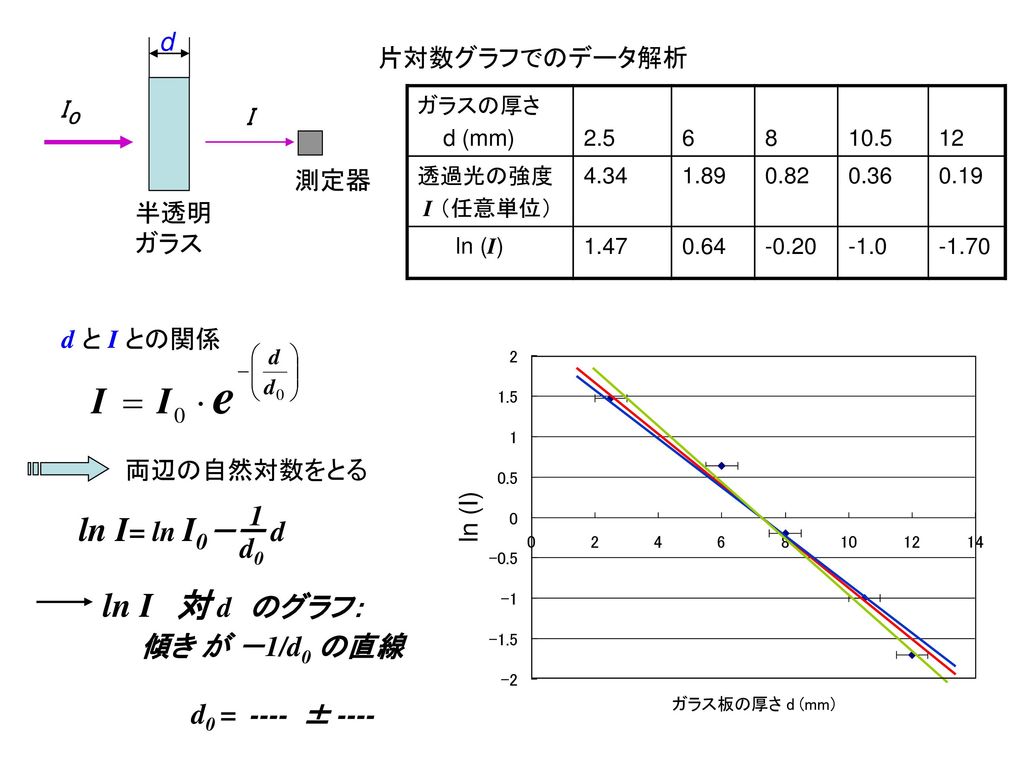



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download



ある薬物300mgをヒトに静脈内投与したところ 下の片対数グ Yahoo 知恵袋



電気基礎実験 グラフ処理 Ppt Download




対数グラフ Todoroki18 Note



電気基礎実験 グラフ処理 Ppt Download




Wo17 号 鋼部品 Astamuse




片対数グラフはやめてほしい Qiita



新型コロナウィルス 中国と韓国では初期には指数関数的増加が起きているものの あるポイントを超えると増加率が低下し始める 新型コロナ 増加が終息するポイント ビジネスジャーナル
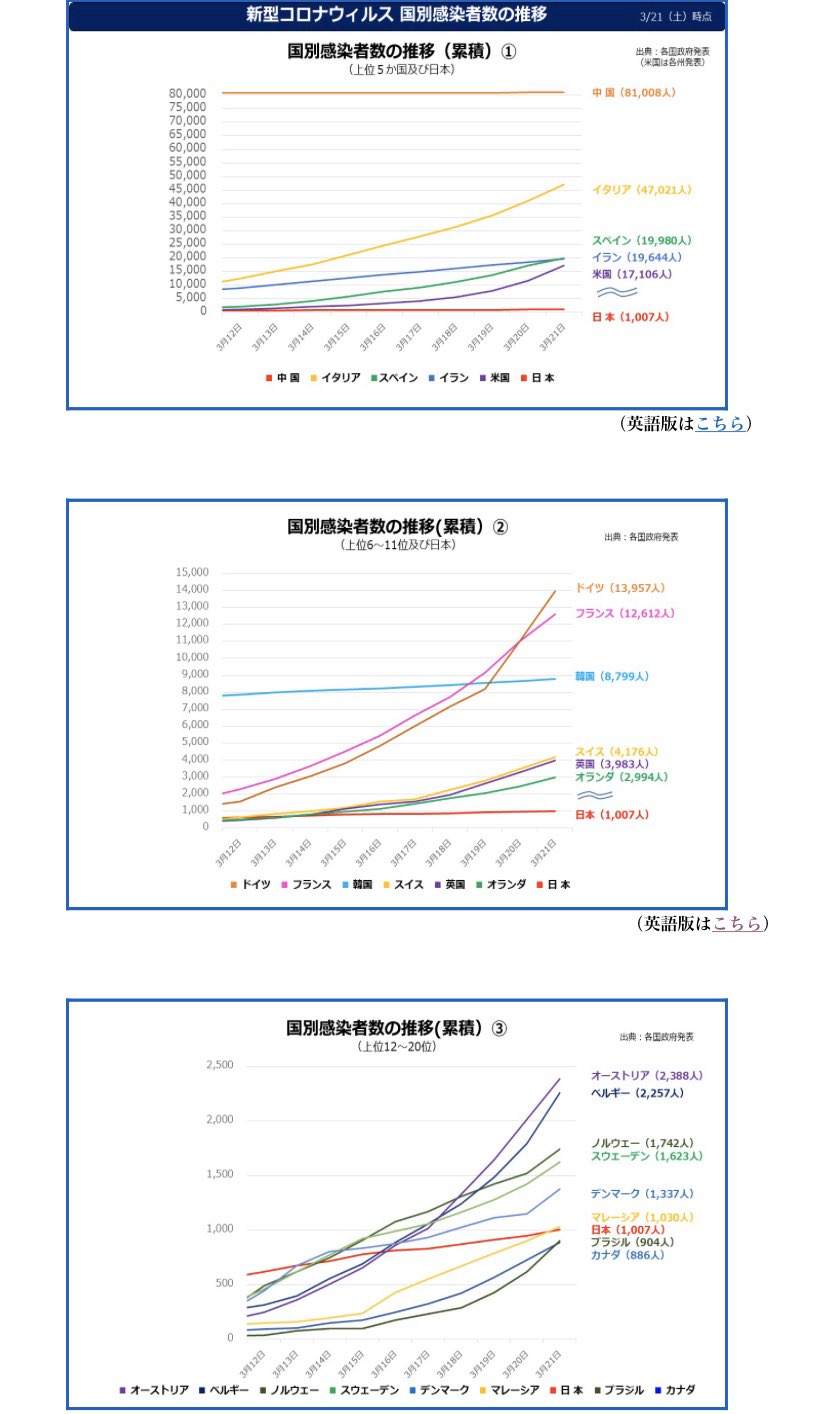



涅槃 旧びのまる 片対数グラフでなければこのように分けて書くグラフ でシンプルに増加数 増加率の各国比較ができますね 日本と韓国はほぼ同様の傾きを保っています イタリア アメリカヤバいですがドイツ フランスもアメリカとほぼ同じです
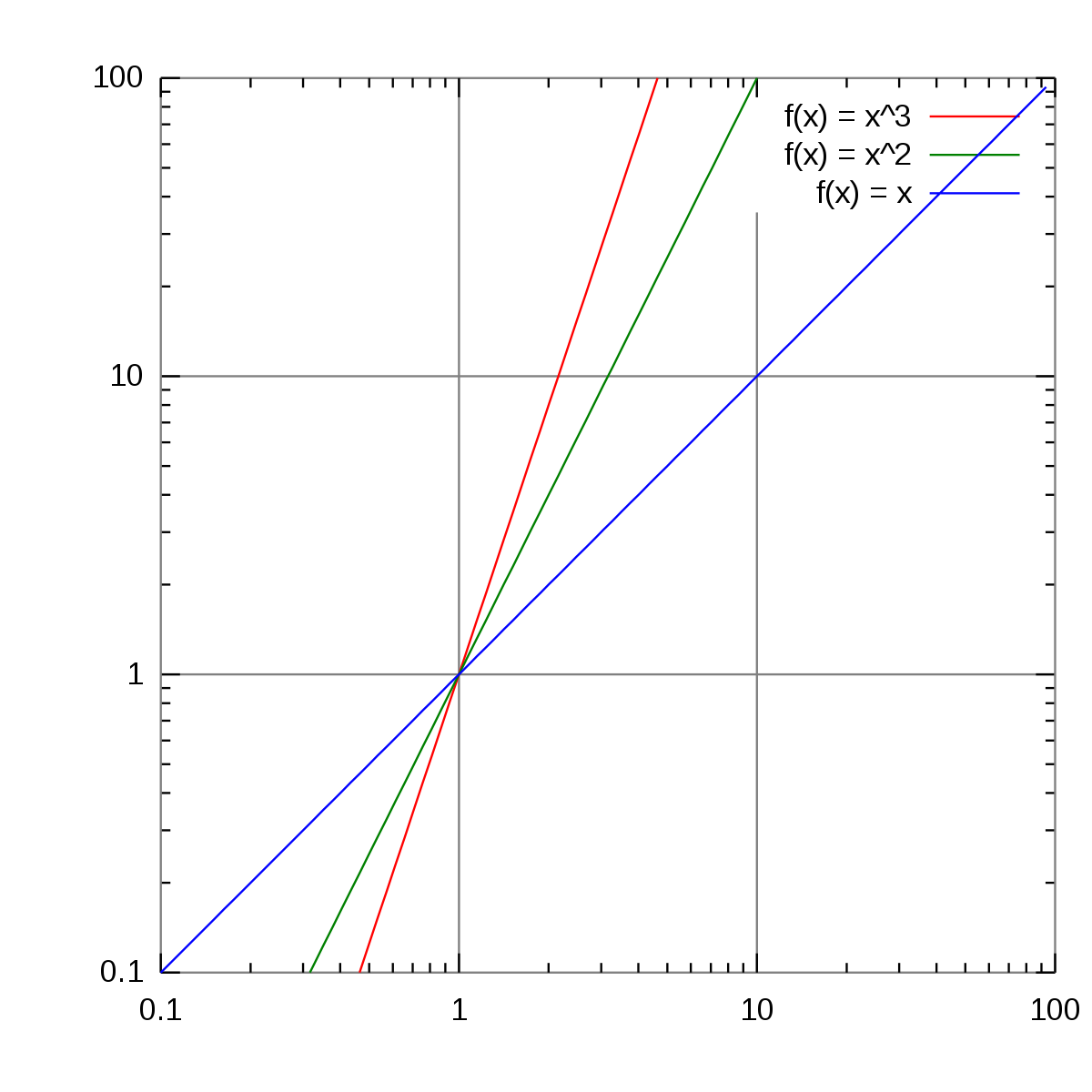



両対数グラフ Wikipedia
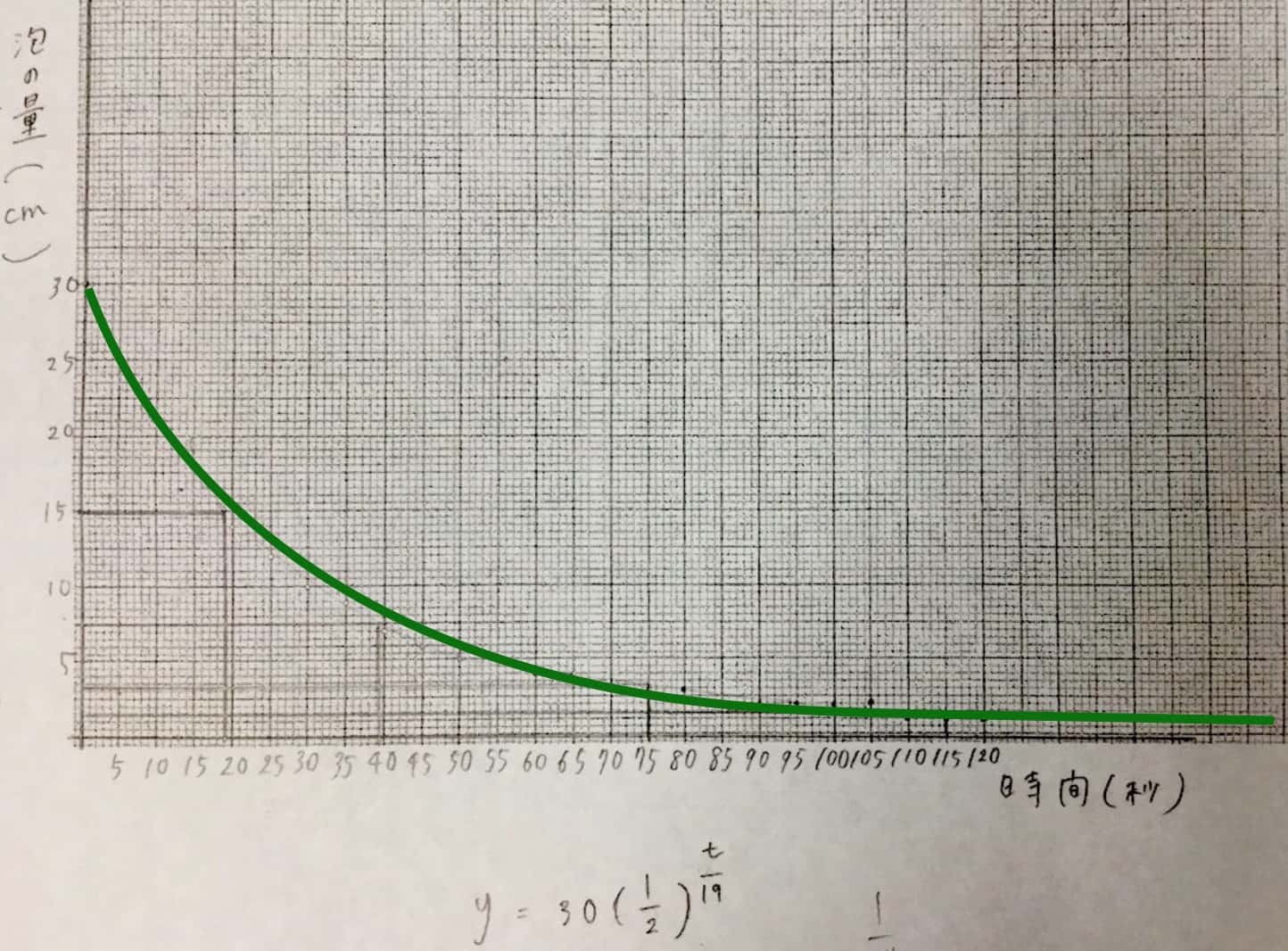



新型コロナウィルスで考える指数関数的な変化と自然現象 科学のネタ帳
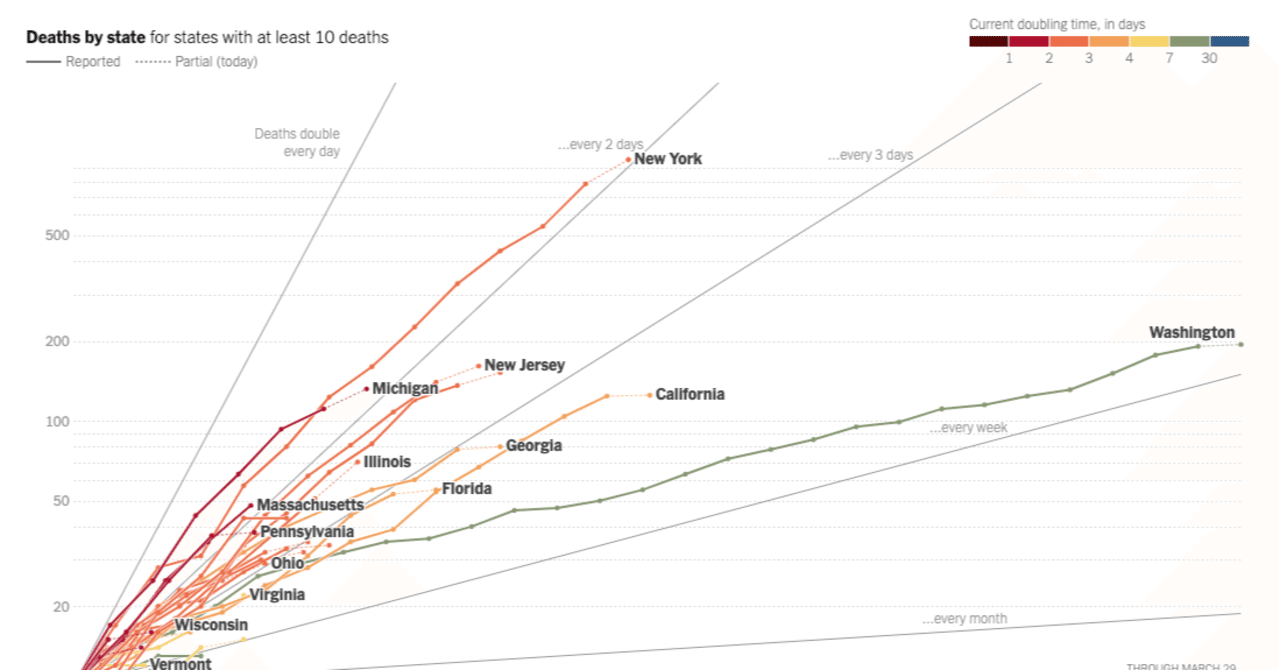



新型コロナウイルスの感染者数の増減を片対数グラフで表す理由 矢崎 裕一 Note
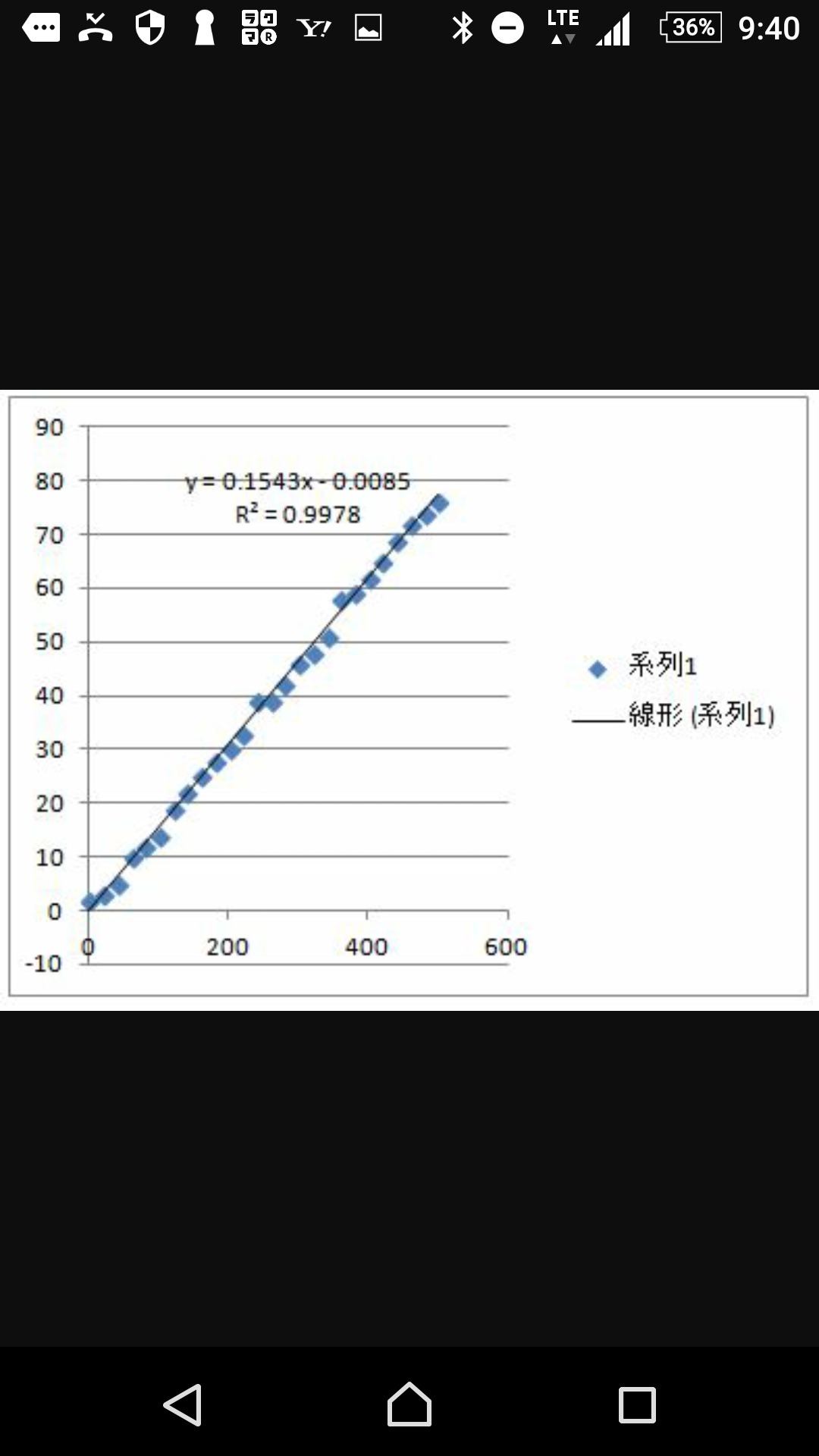



エクセルで大変困ったことがあります 至急 Okwave




グーテンベルグ リヒター則 Wikipedia




ワトソン 4 4 東京の新規感染者が初の3桁突入と話題になったが 見事に直線に乗っていて 別に驚くに値しないことだったということがわかる 容易に予測できたこと



エクセル 片 対数 グラフ 作り方




対数目盛の意味 用法を知る Astamuse




黒羽音響技研の実験室 日記



緩和現象 けての物理 Rtmよも急発信所



電気基礎実験 グラフ処理 Ppt Download



電気基礎実験 グラフ処理 Ppt Download




結城由羅 世界忍者国 世界というか イタリアとアメリカと日本とプラスアルファの100万人あたり死亡数推移 片対数 04 05 イタリアはだいぶ落ち着いてきた それでも230とは けど アメリカは相変わらず指数関数的に増大中 日本はちびっと上に向き




Images Of 片対数グラフ Japaneseclass Jp



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先



0 件のコメント:
コメントを投稿